题目内容
【题目】已知![]()
(1)求![]() 的轨迹
的轨迹![]()
(2)过轨迹![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线
的切线![]() ,设直线
,设直线![]() 的斜率分别是
的斜率分别是![]() ,试问在三个斜率都存在且不为0的条件下,
,试问在三个斜率都存在且不为0的条件下, 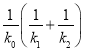 是否是定值,请说明理由,并加以证明.
是否是定值,请说明理由,并加以证明.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:
(1)利用几何性质取得该轨迹方程为椭圆,求得![]() 即可得出该轨迹方程;也可以利用平面向量的结论结合坐标求解轨迹方程;
即可得出该轨迹方程;也可以利用平面向量的结论结合坐标求解轨迹方程;
(2)利用题意联立直线与椭圆的方程,结合韦达定理证得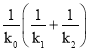 是定值即可.
是定值即可.
试题解析:
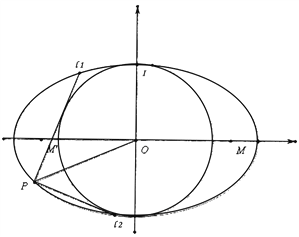
(1)方法一:
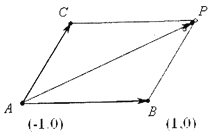
如图因为![]() 所以四边形
所以四边形![]() 是平行四边形
是平行四边形
所以![]() ,
,
由![]() 得
得![]()
所以![]() 的轨迹是以
的轨迹是以![]() 为焦点的椭圆易知
为焦点的椭圆易知![]()
![]()
所以方程为![]()
方法二:
设![]() 由
由![]() 得
得![]()
再![]() 得
得
![]()
移项![]()
平方化简得: ![]()
(从![]() 发现是椭圆方程也可以直接得
发现是椭圆方程也可以直接得![]()
![]() ,分档批阅老师自己把握)
,分档批阅老师自己把握)
(2)设![]() ,过
,过![]() 的斜率为
的斜率为![]() 的直线为
的直线为![]() ,由直线与圆
,由直线与圆![]() 相切可得
相切可得
![]()
即: ![]()
由已知可知![]() 是方程(关于
是方程(关于![]() )
)![]() 的两个根,
的两个根,
所以由韦达定理:

两式相除: ![]()
又因为![]() 所以
所以![]()
代入上式可得: ![]() 即:
即: 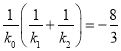 为一个定值.
为一个定值.

练习册系列答案
相关题目