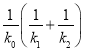题目内容
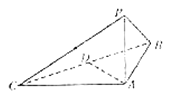
【题目】已知四面体![]() 的棱长满足
的棱长满足![]() ,
,![]() ,现将四面体
,现将四面体![]() 放入一个主视图为等边三角形的圆锥中,使得四面体
放入一个主视图为等边三角形的圆锥中,使得四面体![]() 可以在圆锥中任意转动,则圆锥侧面积的最小值为___________.
可以在圆锥中任意转动,则圆锥侧面积的最小值为___________.
【答案】![]()
【解析】
若满足题意,则四面体的外接球应该内切于圆锥即可.先求得四面体外接球的半径,再根据该球内切于圆锥,即可求得圆锥侧面积的最小值.
若满足题意,则四面体的外接球应该内切于圆锥即可.
为逻辑清晰,我们将问题主要分为两步.
第一步:求得四面体![]() 外接球半径.
外接球半径.
记![]() 外心为
外心为![]() ,过
,过![]() 作平面
作平面![]() 的垂线
的垂线![]() ,
,
记外接球球心为![]() ,连接
,连接![]() .
.
则外接球半径![]() .下面求解
.下面求解![]() .
.

在![]() 中,由余弦定理可得
中,由余弦定理可得![]() ,
,
则由同角三角函数关系可得![]() .
.
故![]() 外接圆半径
外接圆半径![]() .
.
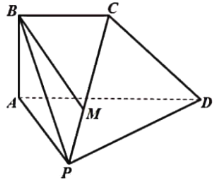
将![]() 的图形单独抽取出来,取
的图形单独抽取出来,取![]() 中点为
中点为![]() .如上面由图所示:
.如上面由图所示:
容易知: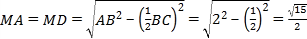 .
.
在![]() 中,因为
中,因为![]() ,
,![]() ,
,
故可得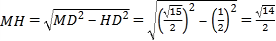 ,
,
![]() .
.
故可得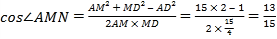 .
.
又因为![]() ,
,
解得![]() .
.
在![]() 中,容易得
中,容易得![]() .
.
故可得![]() .
.
在![]() 中,
中,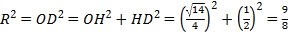 .
.
故可得四面体![]() 外接球半径
外接球半径![]() .
.
第二步:根据外接球半径和圆锥的关系,求得圆锥的母线和底面圆半径.
若满足题意,则该外接球应该内切于圆锥,
作出轴截面的平面图,其中![]() 点为
点为![]() 的中点,如下所示:
的中点,如下所示:

该截面图中![]() .
.
由题可知![]() 为等边三角形,故可得
为等边三角形,故可得![]() ;
;
在![]() 中,
中,![]() ,解得
,解得![]() .
.
故可得圆锥的底面圆半径为![]() .母线长
.母线长![]() .
.
故可得圆锥的侧面积为![]()
![]() .
.
故答案为:![]() .
.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目