题目内容
3.命题p:?α∈R,cos(π+α)=cosα,命题q:?x∈R,x2+1>0,则下面结论正确的是( )| A. | p是假命题 | B. | ¬q是真命题 | C. | p∨q是假命题 | D. | p∨q是真命题 |
分析 分别判定命题p与q的真假,再利用复合命题之间的判定方法即可得出.
解答 解:∵命题p:?α∈R,cos(π+α)=cosα,是真命题,例如取α=$\frac{π}{2}$;
命题q:?x∈R,x2+1>0,是真命题.
因此:只有p∨q是真命题.
故选:D.
点评 本题考查了三角函数求值、函数的性质、复合命题之间的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知命题p:对任意x∈R,都有x2+1>0,则命题p的否定为( )
| A. | 存在x0∈R,使得${x_0}^2+1>0$ | B. | 存在x0∈R,使得${x_0}^2+1≤0$ | ||
| C. | 存在x0∈R,使得${x_0}^2+1<0$ | D. | 存在x0∈R,使得${x_0}^2+1≥0$ |
8.通过市场调查知某商品每件的市场价y(单位:圆)与上市时间x(单位:天)的数据如下:
根据上表数据,当a≠0时,下列函数:①y=ax+k;②y=ax2+bx+c;③y=alogmx中能恰当的描述该商品的市场价y与上市时间x的变化关系的是(只需写出序号即可)②.
| 上市时间x天 | 4 | 10 | 36 |
| 市场价y元 | 90 | 51 | 90 |
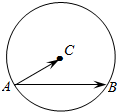 如图,定圆C的半径为4,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|{\overrightarrow{AB}-t\overrightarrow{AC}}|≥|{\overrightarrow{BC}}|$对任意的t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=16.
如图,定圆C的半径为4,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|{\overrightarrow{AB}-t\overrightarrow{AC}}|≥|{\overrightarrow{BC}}|$对任意的t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=16. 我校在高三某班参加夏令营的12名同学中,随机抽取6名,统计他们在参加夏令营期间完成测试项目的个数,并制成茎叶图如图所示,其中茎为十位数,叶为个位数
我校在高三某班参加夏令营的12名同学中,随机抽取6名,统计他们在参加夏令营期间完成测试项目的个数,并制成茎叶图如图所示,其中茎为十位数,叶为个位数