题目内容
19．若实数x，y满足约束条件$\left\{\begin{array}{l}{x+y-1≥0}\\{x-1≤0}\\{4x-y+1≥0}\end{array}\right.$则目标函数z=$\frac{y+1}{x+3}$的最大值为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{2}$ | D． | 2 |
分析 作出不等式组对应的平面区域，利用斜率的几何意义，进行求解即可．
解答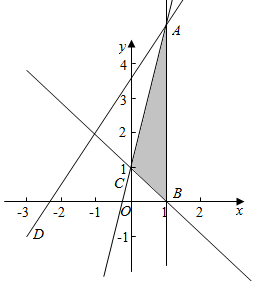 
解：作出不等式组对应的平面区域，
z=$\frac{y+1}{x+3}$的几何意义是区域内的点到点D（-3，-1）的斜率，
由图象知AD的斜率最大，
由$\left\{\begin{array}{l}{4x-y+1=0}\\{x-1=0}\end{array}\right.$，得$\left\{\begin{array}{l}{x=1}\\{y=5}\end{array}\right.$，即A（1，5），
则z=$\frac{y+1}{x+3}$的最大值z=$\frac{5+1}{1+4}$=$\frac{6}{4}$=$\frac{3}{2}$，
故选：C．
点评 本题主要考查线性规划的应用，根据两点之间的斜率公式以及数形结合是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
14．若m＜0，则直线2mx-m2y-y+3=0的倾斜角的范围是（ ）
| A． | [0，$\frac{π}{4}$] | B． | [$\frac{π}{4}$，$\frac{π}{2}$） | C． | （$\frac{π}{2}$，$\frac{3π}{4}$] | D． | [$\frac{3π}{4}$，π） |
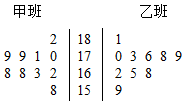从某中学的甲乙两个班中各随机抽取10名同学，分别测量他们的身高（单位：cm），得到身高数据的茎叶图如图所示，若从乙班被抽取的这10名同学中再随机抽取2名身高不低于173cm的同学，则身高为176cm的同学被抽到的概率为$\frac{2}{5}$．