题目内容
2.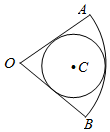 如图,圆C内切于扇形AOB,∠AOB=$\frac{π}{3}$,若向扇形AOB内随机投掷300个点,则落入圆内的点的个数估计值为( )
如图,圆C内切于扇形AOB,∠AOB=$\frac{π}{3}$,若向扇形AOB内随机投掷300个点,则落入圆内的点的个数估计值为( )| A. | 450 | B. | 400 | C. | 200 | D. | 100 |
分析 本题是一个等可能事件的概率,试验发生包含的事件对应的包含的事件对应的是扇形AOB,满足条件的事件是圆,根据题意,构造直角三角形求得扇形的半径与圆的半径的关系,进而根据面积的求法求得扇形OAB的面积与⊙P的面积比,可得概率,即可得出结论..
解答  解:由题意知本题是一个等可能事件的概率,设圆C的半径为r,
解:由题意知本题是一个等可能事件的概率,设圆C的半径为r,
试验发生包含的事件对应的是扇形AOB,
满足条件的事件是圆,其面积为⊙C的面积=π•r2,
连接OC,延长交扇形于P.
由于CE=r,∠BOP=$\frac{π}{6}$,OC=2r,OP=3r,
则S扇形AOB=$\frac{π•(3r)^{2}}{6}$=$\frac{3π{r}^{2}}{2}$;
∴⊙C的面积与扇形OAB的面积比是$\frac{2}{3}$.
∴概率P=$\frac{2}{3}$,
∵向扇形AOB内随机投掷300个点,
∴落入圆内的点的个数估计值为300×$\frac{2}{3}$=200.
故选C.
点评 本题是一个等可能事件的概率,对于这样的问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果.连接圆心和切点是常用的辅助线做法,本题的关键是求得扇形半径与圆半径之间的关系.

练习册系列答案
相关题目
7.菱形ABCD的边长为3,DC=3DE,若$\overrightarrow{AD}•\overrightarrow{AB}$=$\frac{9}{2}$,则$\overrightarrow{AE}$•$\overrightarrow{AC}$=( )
| A. | 15 | B. | 18 | C. | 21 | D. | 24 |
14.若m<0,则直线2mx-m2y-y+3=0的倾斜角的范围是( )
| A. | [0,$\frac{π}{4}$] | B. | [$\frac{π}{4}$,$\frac{π}{2}$) | C. | ($\frac{π}{2}$,$\frac{3π}{4}$] | D. | [$\frac{3π}{4}$,π) |
12.若函数f(x)=sinωx+cosωx(ω>0)的图象相邻两条对称轴之间的距离为3,则ω值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |