题目内容
求函数f(x)=x2+x-2-a(x+x-1)+a+2(x>0)的最小值.
考点:函数的最值及其几何意义,有理数指数幂的化简求值
专题:计算题,函数的性质及应用
分析:化简f(x)=x2+x-2-a(x+x-1)+a+2=(x+x-1)2-a(x+x-1)+a;从而令z=x+x-1,则z≥2;配方法得y=z2-az+a=(z-
)2+a-
;从而求最小值.
| a |
| 2 |
| a2 |
| 4 |
解答:
解:f(x)=x2+x-2-a(x+x-1)+a+2
=(x+x-1)2-a(x+x-1)+a;
令z=x+x-1,则z≥2;
y=z2-az+a=(z-
)2+a-
;
当
≤2,即a≤4时,
ymin=4-2a+a=4-a;
当
>2,即a>4时,
ymin=a-
.
=(x+x-1)2-a(x+x-1)+a;
令z=x+x-1,则z≥2;
y=z2-az+a=(z-
| a |
| 2 |
| a2 |
| 4 |
当
| a |
| 2 |
ymin=4-2a+a=4-a;
当
| a |
| 2 |
ymin=a-
| a2 |
| 4 |
点评:本题考查了换元法及配方法求函数的最小值,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设x,y满足约束条件
,则z=x+2y的最小值为( )
|
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
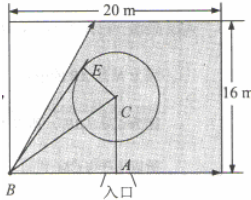
 如图,已知实数t满足t∈(0,10),由t确定的两个任意点P(t,t),Q(10-t,0),问:
如图,已知实数t满足t∈(0,10),由t确定的两个任意点P(t,t),Q(10-t,0),问: