题目内容
求证:m
=n
(m≤n,m,n∈N+).
| C | m n |
| C | m-1 n-1 |
考点:组合及组合数公式
专题:排列组合
分析:根据组合数公式
=
,代入化简即可.
| C | m n |
| n! |
| m!•(n-m)! |
解答:
证明:当m≤n,且m,n∈N+时,
m
=m•
=n•
=n
.
m
| C | m n |
| n! |
| m!•(n-m)! |
=n•
| (n-1)! |
| (m-1)!•[(n-1)-(m-1)]! |
=n
| C | m-1 n-1 |
点评:本题考查了组合数公式的应用问题,是基础题目.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
已知x,y满足:x+y=
且x,y≠kπ+
(k∈Z),则(1+tanx)(1+tany)=( )
| π |
| 4 |
| π |
| 2 |
| A、-2 | B、2 | C、-1 | D、1 |
数列{an}满足an=n2+kn+2,若不等式an≥a4恒成立,则实数k的取值范围是( )
| A、[-9,-8] |
| B、[-9,-7] |
| C、(-9,-8) |
| D、(-9,-7) |
当x∈[-3,0]时,函数y=x2+2x+3的最小值是( )
| A、1 | B、2 | C、3 | D、4 |
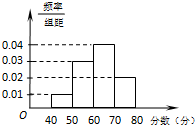 在我市2015年“创建文明城市”知识竞赛中,考评组从中抽取200份试卷进行分析,其分数的频率分布直方图如图所示,则分数在区间[60,70)上的人数大约有
在我市2015年“创建文明城市”知识竞赛中,考评组从中抽取200份试卷进行分析,其分数的频率分布直方图如图所示,则分数在区间[60,70)上的人数大约有