题目内容
6.方程log5x+x-2=0的根所在的区间是( )| A. | (2,3) | B. | (1,2) | C. | (3,4) | D. | (0,1) |
分析 方程的根转化为函数的零点,判断函数的连续性以及单调性,然后利用零点判定定理推出结果即可.
解答 解:方程log5x+x-2=0的根就是y=log5x+x-2的零点,
函数是连续函数,是增函数,
可得f(1)=0+1-2=-1<0,f(2)=log52+2-2>0,
所以f(1)f(2)<0,
方程根在(1,2).
故选:B.
点评 本题考查函数的零点判定定理的应用,考查计算能力.

练习册系列答案
相关题目
1.全集U=R,集合A={-1,0,1},B={x|$\frac{x-2}{x+1}$>0},则A∩(∁UB)=( )
| A. | {0,1} | B. | {0,1,2} | C. | {-1,0,1} | D. | ∅ |
16.在平面几何中,可以得出正确结论:“正三角形的内切圆半径等于这个正三角形的高的$\frac{1}{3}$.”拓展到空间中,类比平面几何的上述结论,则正四面体的内切球半径等于这个正四面体的高的( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |
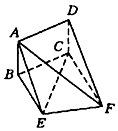 如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF,∠BCF=∠CEF=90°.AD=$\sqrt{3}$,EF=2
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF,∠BCF=∠CEF=90°.AD=$\sqrt{3}$,EF=2