题目内容
12.已知函数f(x)=mlnx+8x-x2在[1,+∞)上单调递减,则实数m的取值范围为( )| A. | (-∞,-8] | B. | (-∞,-8) | C. | (-∞,-6] | D. | (-∞,-6) |
分析 求出函数的导数,得到m≤2x2-8x在[1,+∞),令h(x)=2x2-8x,x∈[1,+∞),根据函数的单调性求出m的范围即可.
解答 解:f′(x)=$\frac{m}{x}$+8-2x=$\frac{-{2x}^{2}+8x+m}{x}$,
令g(x)=-2x2+8x+m,
若函数f(x)=mlnx+8x-x2在[1,+∞)上单调递减,
则-2x2+8x+m≤0在[1,+∞)成立,
则m≤2x2-8x在[1,+∞),
令h(x)=2x2-8x,x∈[1,+∞),
h′(x)=4x-8,令h′(x)>0,解得:x>2,
令h′(x)<0,解得:1≤x<2,
故h(x)在[1,2)递减,在(2,+∞)递增,
故h(x)min=h(2)=-8,
故m≤-8,
故选:A.
点评 本题考查了函数的单调性问题,考查导数的应用以及转化思想,是一道中档题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
3.设x∈R,则“|x-1|<2”是“x2-4x-5<0”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.若向量$\overrightarrow a=(sin2α,cosα),\overrightarrow b=(1,cosα)$,且$tanα=\frac{1}{2}$,则$\overrightarrow a•\overrightarrow b$的值是( )
| A. | $\frac{8}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{4}{5}$ | D. | 2 |
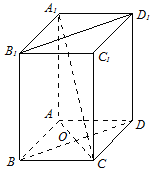 已知长方体A1B1C1D1-ABCD的高为$\sqrt{2}$,两个底面均为边长为1的正方形.
已知长方体A1B1C1D1-ABCD的高为$\sqrt{2}$,两个底面均为边长为1的正方形.