题目内容
4.函数f(x)=x5+ax4-bx2+1,其中a是1202(3)对应的十进制数,b是8251与6105的最大公约数,试应用秦九韶算法求当x=-1时V3的值.分析 由进位制知:a=47.应用辗转相除法可得:b=37.利用秦九韶算法可得:f(x)=x5+ax4-bx2+1=x5+47x4-37x2+1=(((x+47)x)x-37)x+1,即可得出.
解答 解:由进位制知:a=1×33+2×32+0×31+2×30=47.
应用辗转相除法可得:8251=6105+2146,6105=2146×2+1813,2146=1813+333,1813=333×5+148,333=148×2+37,148=37×4.
∴8251与6105的最大公约数为37,因此b=37.
利用秦九韶算法可得:f(x)=x5+ax4-bx2+1=x5+47x4-37x2+1=(((x+47)x)x-37)x+1,
V0=1,V1=V0x+47=46,V2=V1x+0=-46,V3=V2x-37=9.
点评 本题考查了进位制、辗转相除法、秦九韶算法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.在边长为1的正三角形ABC中,设D,E分别为AB,AC的中点,则$\overrightarrow{BE}$•$\overrightarrow{CD}$=( )
| A. | -$\frac{3}{16}$ | B. | -$\frac{3}{8}$ | C. | -$\frac{3}{4}$ | D. | 0 |
 某学生对其30位亲属的饮食习惯进行了一次调查,并用茎叶图表示30人的饮食指数.说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.
某学生对其30位亲属的饮食习惯进行了一次调查,并用茎叶图表示30人的饮食指数.说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.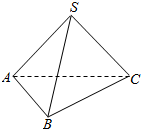 如图,在棱长都相等的四面体SABC中,给出如下三个命题:
如图,在棱长都相等的四面体SABC中,给出如下三个命题: