题目内容
14．若${∫}_{1}^{2}$（x-a）dx=${∫}_{0}^{\frac{π}{6}}$cosxdx，则a等于（ ）| A． | -1 | B． | 1 | C． | 2 | D． | 4 |
分析 利用定积分的运算法则列出方程，求出a的值即可．
解答 解：∵$\int_1^2{（{x-a}）}dx=\int_0^{\frac{π}{6}}{cosxdx}$，
∴（$\frac{1}{2}$x2-ax）${|}_{1}^{2}$=sinx${|}_{0}^{\frac{π}{6}}$，
即$\frac{3}{2}$-a=$\frac{1}{2}$，
解得a=1．
故选：B．
点评 本题考查了定积分的求法问题，求出积分函数的原函数是解题的关键，是基础题．
练习册系列答案
相关题目
5．某班同学利用国庆节进行社会实践，对[20，50]岁的临汾市“低头族”（低头族电子产品而忽视人际交往的人群）人群随是因使用机抽取1000人进行了一次调查，得到如下频数分布表：
（1）在答题卡上作出这些数据的频率分布直方图；
（2）估计[20，50]年龄段的“低头族”的平均年龄（同一组中的数据用该组区间的中点值作代表）；
（3）从年龄段在[25，35）的“低头族”中采用分层抽样法抽取6人接受采访，并从6人中随机选取2人作为嘉宾代表，求选取的2名嘉宾代表中恰有1人年龄在[25，30）岁的概率．
| 年龄段分组 | [20，25） | [25，30） | [30，35） | [35，40） | [40，45） | [45，50] |
| 频数 | 300 | 320 | 160 | 160 | 40 | 20 |
（2）估计[20，50]年龄段的“低头族”的平均年龄（同一组中的数据用该组区间的中点值作代表）；
（3）从年龄段在[25，35）的“低头族”中采用分层抽样法抽取6人接受采访，并从6人中随机选取2人作为嘉宾代表，求选取的2名嘉宾代表中恰有1人年龄在[25，30）岁的概率．
2．准线为x=-2的抛物线的标准方程为（ ）
| A． | y2=-8x | B． | y2=8x | C． | x2=8y | D． | x2=-8y |
6．如图是一个几何体的三视图，则该几何体的体积等于（ ）
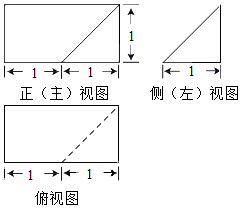
| A． | $\frac{1}{2}$ | B． | $\frac{5}{6}$ | C． | 1 | D． | $\frac{5}{3}$ |
3．
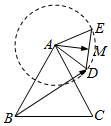如图，等边△ABC的边长为2，△ADE也是等边三角形且边长为1，M为DE的中心，在△ABC所在平面内，△ADE绕A逆时针旋转一周，$\overrightarrow{BD}$•$\overrightarrow{AM}$的最大值为（ ）
如图，等边△ABC的边长为2，△ADE也是等边三角形且边长为1，M为DE的中心，在△ABC所在平面内，△ADE绕A逆时针旋转一周，$\overrightarrow{BD}$•$\overrightarrow{AM}$的最大值为（ ）| A． | $\frac{3}{4}$ | B． | $\frac{3}{4}$+$\sqrt{3}$ | C． | $\frac{3+\sqrt{3}}{4}$ | D． | $\frac{3}{4}$+2$\sqrt{3}$ |