题目内容
3．若命题p：已知0＜a＜1，?x＜0，ax＞1，则￢p为（ ）| A． | 已知a＞1，?x＞0，ax≤1 | B． | $已知0＜a＜1，?{x_0}＜0，{a^{x_0}}≤1$ | ||
| C． | $已知0＜a＜1，?{x_0}≥0，{a^{x_0}}≤1$ | D． | 已知a＞1，?x＞0，ax≤1 |
分析 直接利用全称命题的否定是特称命题写出结果即可．
解答 解：因为全称命题的否定是特称命题，所以命题p：已知0＜a＜1，?x＜0，ax＞1，则￢p：$已知0＜a＜1，?{x_0}＜0，{a^{x_0}}≤1$，
故选：B
点评 本题考查命题的否定，全称命题与特称命题的否定关系，基本知识的考查．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
13．圆（x-1）2+（y+1）2=10的半径为（ ）
| A． | （1，-1） | B． | （-1，1） | C． | $\sqrt{10}$ | D． | 10 |
14．某多面体的三视图如下图所示（网格纸上小正方形的边长为1），则该多面体的表面积为（ ）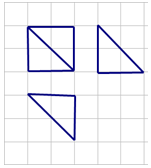
| A． | $8+4\sqrt{2}$ | B． | $6+4\sqrt{2}$ | C． | 12 | D． | $8+5\sqrt{2}$ |
11．
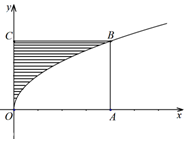如图，长方形OABC中，O为坐标原点，点C在y轴上，A（4，0），曲线y2=ax（a＞0）经过点B，现将一质点随机投入长方形OABC中，若质点落在图中阴影区域的概率是（ ）
如图，长方形OABC中，O为坐标原点，点C在y轴上，A（4，0），曲线y2=ax（a＞0）经过点B，现将一质点随机投入长方形OABC中，若质点落在图中阴影区域的概率是（ ）| A． | 2 | B． | 1 | C． | $\frac{1}{3}$ | D． | $\frac{2}{3}$ |
18．曲线y=x•ex在x=1处切线的斜率等于（ ）
| A． | 2e | B． | e | C． | 2 | D． | 1 |
8．已知A（-1，0），B（3，2），C（0，-2），则过这三点的圆方程为（ ）
| A． | （x-$\frac{3}{2}$）2+y2=25 | B． | （x+$\frac{3}{2}$）2+y2=$\frac{1}{4}$ | C． | （x-$\frac{3}{2}$）2+y2=$\frac{25}{4}$ | D． | x2+（y-$\frac{3}{2}$）2=$\frac{5}{2}$ |
15．已知向量$\overrightarrow a=（2cosθ，2sinθ），\overrightarrow b=（0，-2）$，$θ∈（\frac{π}{2}，π）$，则向量夹角为（ ）
| A． | $\frac{3π}{2}-θ$ | B． | $θ-\frac{π}{2}$ | C． | $\frac{π}{2}+θ$ | D． | θ |
12．在区间[-1，3]上随机取一个数x，若x满足|x|＜m的概率为0.75，则m=（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
如图，已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0），点A，B分别是左、右顶点，过右焦点F的直线MN（异于x轴）交于椭圆C于M、N两点．