题目内容
已知x,y满足约束条件
,且z=2x+4y的最小值为6,则常数k= ;z=2x+4y的最大值是 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出可行域,变形目标函数,平移直线y=-
x可知当直线经过点A(3,-3-k)时,目标函数取最小值,可得k值,又可得当直线经过点B(3,9)时,目标函数取最大值,代值计算可得.
| 1 |
| 2 |
解答:
解:作出约束条件
所对应的可行域(如图阴影),
变形目标函数可得y=-
x+
z,平移直线y=-
x可知
当直线经过点A(3,-3-k)时,目标函数取最小值,
∴2×3+4(-3-k)=6,解得k=-3,
当直线经过点B(3,9)时,目标函数取最大值zmax=42
故答案为:-3;42

|
变形目标函数可得y=-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
当直线经过点A(3,-3-k)时,目标函数取最小值,
∴2×3+4(-3-k)=6,解得k=-3,
当直线经过点B(3,9)时,目标函数取最大值zmax=42
故答案为:-3;42

点评:本题考查简单线性规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
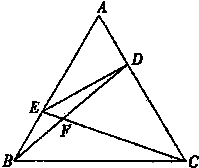 如图,在正三角形ABC中,点D,E分别在边AC,AB上,且AD=
如图,在正三角形ABC中,点D,E分别在边AC,AB上,且AD=