题目内容
从半径R的球内接正方体的8个顶点及球心这9个点中任取2个点,则这两个点间的距离小于或等于半径的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计,排列组合
分析:画出正方体的图形,设正方体的边长为1,求出正方形的外接球半径R=
;
计算从9个点中任取2个点的取法种数以及所取的2个点间的距离小于或等于半径的取法种数,求出对应的概率即可.
| ||
| 2 |
计算从9个点中任取2个点的取法种数以及所取的2个点间的距离小于或等于半径的取法种数,求出对应的概率即可.
解答:
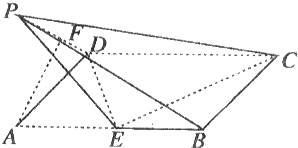
 解:如图所示,
解:如图所示,
设正方体的边长为1,则该正方形的外接球的直径为
,半径R=
;
∴从球内接正方体的8个顶点及球心这9个点中任取2个点,方法有
=36种;
其中这两个点间的距离小于半径的取法有0种,
等于半径的取法有8种,是OA、OB、OC、OD、OA1、OB1、OC1、OD1,
共0+8=8种;
∴所求的概率为P=
=
.
故选:B.
 解:如图所示,
解:如图所示,设正方体的边长为1,则该正方形的外接球的直径为
| 3 |
| ||
| 2 |
∴从球内接正方体的8个顶点及球心这9个点中任取2个点,方法有
| C | 2 9 |
其中这两个点间的距离小于半径的取法有0种,
等于半径的取法有8种,是OA、OB、OC、OD、OA1、OB1、OC1、OD1,
共0+8=8种;
∴所求的概率为P=
| 8 |
| 36 |
| 2 |
| 9 |
故选:B.
点评:本题考查了古典概型的应用问题,也考查了组合数的应用问题,是基础题目.

练习册系列答案
相关题目
某空间几何体的三视图如图所示,则该几何体的体积是( )


| A、4 | B、5 | C、6 | D、7 |