题目内容
已知椭圆E的中心在坐标原点，焦点在x轴上，离心率为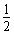
，且椭圆E上一点到两个焦点距离之和为4，l1，l2是过点P(0，2)且互相垂直的两条直线，l1交E于A，B两点，l2交E于C，D两点，AB，CD的中点分别为M，N，
(1)求椭圆E的方程；
(2)求l1的斜率k的取值范围；
(3)求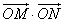
的取值范围．
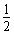，且椭圆E上一点到两个焦点距离之和为4，l1，l2是过点P(0，2)且互相垂直的两条直线，l1交E于A，B两点，l2交E于C，D两点，AB，CD的中点分别为M，N，(1)求椭圆E的方程；
(2)求l1的斜率k的取值范围；
(3)求
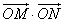的取值范围． 解：(1)设椭圆方程为
，
由
得
，
∴椭圆方程为
。
(2)由题意知，直线l1的斜率存在且不为零，
∵l1：y=kx+2，
∴l2：y=-
x+2，
由
消去y并化简整理，得(3+4k2)x2+16kx+4=0，
根据题意，Δ=(16k)2-16(3+4k2)＞0，解得k2＞
，
同理得
，k2＜4，
∴
＜k2＜4，k∈(-2，-
)∪(
，2)；
(3)设A(x1，y1)，B(x2，y2)，M(x0，y0)，
那么x1+x2=-
，
∴x0=
，y0=kx0+2=
，
∴M
，
同理得N
，即N
，
∴
=
，
∵
＜k2＜4，
∴2≤k2+
，
∴
，
即
的取值范围是
。
，由
得，∴椭圆方程为
。(2)由题意知，直线l1的斜率存在且不为零，
∵l1：y=kx+2，
∴l2：y=-
x+2，由
消去y并化简整理，得(3+4k2)x2+16kx+4=0，根据题意，Δ=(16k)2-16(3+4k2)＞0，解得k2＞
，同理得
，k2＜4，∴
＜k2＜4，k∈(-2，-)∪(，2)；(3)设A(x1，y1)，B(x2，y2)，M(x0，y0)，
那么x1+x2=-
，∴x0=
，y0=kx0+2=，∴M
，同理得N
，即N，∴
=，∵
＜k2＜4，∴2≤k2+
，∴
，即
的取值范围是。
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
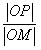=λ，求点M的轨迹方程，并说明轨迹是什么曲线。
，
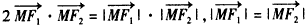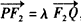，求△PF1Q的内切圆面积最大时实数λ的值．
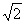，1)到两焦点的距离之和为4
，
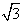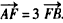，求过O、A、B三点的圆的方程．
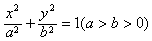的离心率为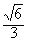
， 
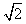，求椭圆的方程；
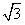时，求b的值；
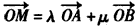，求实数λ、μ满足的关系式。 
（a＞b＞0）的离心率为
，以原点为圆心，椭圆的短半轴长为半径的圆与直线x-y+
=0相切。
（O为坐标原点），当
＜
时，求实数t的取值范围。
的右焦点恰好是抛物线C：y2=4x的焦点F，点A是椭圆E的右顶点，过点A的直线l交抛物线C于M，N两点，满足OM⊥ON，其中O是坐标原点，