题目内容
3．化简：（1+$\frac{1}{ta{n}^{2}θ}$）sin2θ=1．分析 由条件利用同角三角函数的基本关系，求得要求式子的值．
解答 解：：（1+$\frac{1}{ta{n}^{2}θ}$）sin2θ=$\frac{{sin}^{2}θ{+cos}^{2}θ}{{sin}^{2}θ}$•sin2θ=1，
故答案为：1．
点评 本题主要考查同角三角函数的基本关系，属于基础题．
练习册系列答案
相关题目
14．
甲、乙两种商品在过去一段时间内的价格走势如图所示．假设某人持有资金120万元，他可以在t1至t4的任意时刻买卖这两种商品，且买卖能够立即成交（其他费用忽略不计）．如果他在t4时刻卖出所有商品，那么他将获得的最大利润是（ ）
甲、乙两种商品在过去一段时间内的价格走势如图所示．假设某人持有资金120万元，他可以在t1至t4的任意时刻买卖这两种商品，且买卖能够立即成交（其他费用忽略不计）．如果他在t4时刻卖出所有商品，那么他将获得的最大利润是（ ）| A． | 40万元 | B． | 60万元 | C． | 120万元 | D． | 140万元 |
11．已知函数f（x）（对应的曲线连续不断）在区间[0，2]上的部分对应值如表：
由此可判断：当精确度为0.1时，方程f（x）=0的一个近似解为1.41（精确到0.01）
| x | 0 | 0.88 | 1.30 | 1.406 | 1.431 | 1.52 | 1.62 | 1.70 | 1.875 | 2 |
| f（x） | -2 | -0.963 | -0.340 | -0.053 | 0.145 | 0.625 | 1.975 | 2.545 | 4.05 | 5 |
18．下列函数中，既是偶函数又存在零点的是（ ）
| A． | f（x）=sinx | B． | f（x）=x2+1 | C． | f（x）=lnx | D． | f（x）=cosx |
8．在一次数学实验中，运用图形计算器采集到如下一组数据：
则x，y的函数关系与下列哪类函数最接近？（其中a为待定系数，且a＞0）（ ）
| x | 0.25 | 0.50 | 1 | 2.00 | 3.00 | 4.00 |
| y | -1.99 | -1.01 | 0 | 1.01 | 1.58 | 2.01 |
| A． | y=ax | B． | y=ax | C． | y=logax | D． | y=$\frac{a}{x}$ |
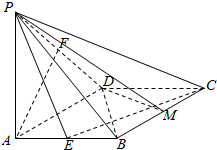如图，在菱形ABCD中，∠DAB=60°，PA⊥底面ABCD，PA=DA，E，F分别是AB、PD的中点．
12．集合P={x∈R||x|≥3，Q={y|y=2x-1，x∈R}，则P∪Q=（ ）
| A． | （-∞，-3]∪（1，+∞） | B． | （-∞，-3]∪（-1，+∞） | C． | （-∞，1）∪[3，+∞） | D． | （-∞，-1）∪[3，+∞） |