题目内容
10．已知$\frac{tanα+1}{5-tanα}=2$，则tana=3 $\frac{sinα+cosα}{sinα-2cosα}$=4．分析 利用“弦化切”即可得出．
解答 解：由$\frac{tanα+1}{5-tanα}=2$，化为3tanα=9，解得tana=3．
$\frac{sinα+cosα}{sinα-2cosα}$=$\frac{tanα+1}{tanα-2}$=$\frac{3+1}{3-2}$=4．
故答案分别为：3；4．
点评 本题考查了“弦化切”、三角函数求值、方程的解法，考查了推理能力与计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
20．设函数$f（x）=cos（{πx-π}）+1，\;\;x∈（{\frac{1}{2}，\frac{3}{2}}）$，若关于x的方程2[f（x）]2-（2a+3）f（x）+3a=0有四个不同的实数解，则满足题意的实数a的取值范围是（ ）
| A． | （0，1） | B． | $（{0，\frac{3}{2}}）$ | C． | （1，2） | D． | $（{1，\frac{3}{2}}）∪（{\frac{3}{2}，2}）$ |
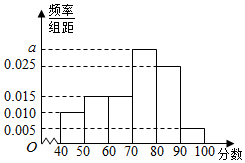某校从参加环保知识竞赛的学生中抽出60名，将其成绩（均为整数）分成六段[40，50），[50，60），…，[90，100]后得到频率分布直方图（如图所示）．
2．复数z=2-4i在复平面内对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |