题目内容
11.某地最近十年粮食需求量逐年上升,如表是部分统计数据:| 年份 | 2002 | 2004 | 2006 | 2008 | 2010 |
| 需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该地2012年的粮食需求量.
提示:线性回归方程y=a+bx,$b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$.
分析 (I)由所给数据看出,年需求量与年份之间是近似直线上升,利用配回归直线方程,对数据预处理,求出预处理后的回归直线方程,从而求出对应的回归直线方程;
(II)利用所求的回归直线方程,计算2012年的粮食需求量即可.
解答 解:(I)由所给数据看出,年需求量与年份之间是近似直线上升,
下面来配回归直线方程,为此对数据预处理如下:
| 年份-2006 | -4 | -2 | 0 | 2 | 4 |
| 需求量-257 | -21 | -11 | 0 | 19 | 29 |
$\overline{x}$=0,$\overline{y}$=3.2,
b=$\frac{(-4)×(-21)+(-2)×(-11)+2×19+4×29}{{(-4)}^{2}{+(-2)}^{2}{+0}^{2}{+2}^{2}{+4}^{2}}$=$\frac{260}{40}$=6.5,
a=$\overline{y}$-b$\overline{x}$=3.2;
由上述计算结果,知所求回归直线方程为
$\stackrel{∧}{y}$-257=b(x-2006)+a=6.5(x-2006)+3.2,
即$\stackrel{∧}{y}$=6.5(x-2006)+260.2;①
(II)利用直线方程①,可预测2012年的粮食需求量为
6.5(2012-2006)+260.2=6.5×6+260.2=299.2(万吨)≈300(万吨).
点评 本题考查了求线性回归方程以及利用回归直线方程预测结果的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.函数y=log4(x+2)的定义域为( )
| A. | {x|x≥-4} | B. | {x|x>-4} | C. | {x|x≥-2} | D. | {x|x>-2} |
16.已知向量$\overrightarrow a=(cosx-sinx,2cosx)$,$\overrightarrow b=(cosx+sinx,sinx)(x∈R)$,则函数$f(x)={(\overrightarrow a•\overrightarrow b)^2}-1$是( )
| A. | 周期为π的偶函数 | B. | 周期为π的奇函数 | ||
| C. | 周期为$\frac{π}{2}$的偶函数 | D. | 周期为$\frac{π}{2}$的奇函数 |
20.设函数$f(x)=cos({πx-π})+1,\;\;x∈({\frac{1}{2},\frac{3}{2}})$,若关于x的方程2[f(x)]2-(2a+3)f(x)+3a=0有四个不同的实数解,则满足题意的实数a的取值范围是( )
| A. | (0,1) | B. | $({0,\frac{3}{2}})$ | C. | (1,2) | D. | $({1,\frac{3}{2}})∪({\frac{3}{2},2})$ |
 已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$在一个周期内的图象,如图所示.
已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$在一个周期内的图象,如图所示.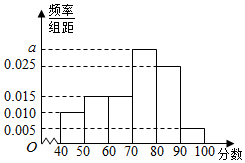 某校从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示).
某校从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示).