题目内容
19.若曲线y=$\frac{1}{2e}$x2与曲线y=alnx在它们的公共点P(s,t)处具有公共切线,则实数a=1.分析 求出两个函数的导数然后求出公共点的斜率,利用斜率相等,有公共点解方程即可求出a的值.
解答 解:曲线y=$\frac{1}{2e}$x2的导数为:y′=$\frac{x}{e}$,
在P(s,t)处的斜率为:k=$\frac{s}{e}$.
曲线y=alnx的导数为:y′=$\frac{a}{x}$,
在P(s,t)处的斜率为:k=$\frac{a}{s}$.
曲线y=$\frac{1}{2e}$x2与曲线y=alnx在它们的公共点P(s,t)处具有公共切线,
可得$\frac{s}{e}$=$\frac{a}{s}$,并且t=$\frac{1}{2e}$s2,t=alns,
即$\left\{\begin{array}{l}{\frac{s}{e}=\frac{a}{s}}\\{\frac{1}{2e}{s}^{2}=alns}\end{array}\right.$,解得lns=$\frac{1}{2}$,解得s2=e.
可得a=1.
故答案为:1.
点评 本题考查函数的导数,导数的几何意义,切线的斜率以及方程思想的运用,考查计算能力,属于中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
14.“m>n>0”是“方程mx2+ny2=1表示焦点在y轴上的椭圆的”( )
| A. | 必要非充分条件 | B. | 充分非必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
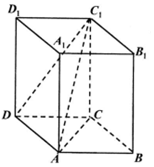 如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC=$\sqrt{3}$,BC=BB1=2.
如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC=$\sqrt{3}$,BC=BB1=2.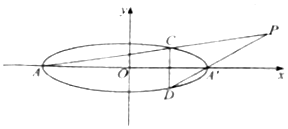 如图所示,椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1的左,右顶点分别为A,A′,线段CD是垂直于椭圆长轴的弦,连接AC,DA′相交于点P,则点P的轨迹方程为$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1.
如图所示,椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1的左,右顶点分别为A,A′,线段CD是垂直于椭圆长轴的弦,连接AC,DA′相交于点P,则点P的轨迹方程为$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1.