题目内容
7．比较${∫}_{0}^{\frac{π}{2}}$sin5xdx与${∫}_{0}^{\frac{π}{2}}$sinxdx的大小．分析 根据定积分的几何意义即可判断．
解答 解：当x∈（0，$\frac{π}{2}$），
∴0＜sinx＜1，
∴sin5x＜sinx，
∴${∫}_{0}^{\frac{π}{2}}$sin5xdx＜${∫}_{0}^{\frac{π}{2}}$sinxdx．
点评 本题主要考查了定积分及其运算，涉及定积分的几何意义和大小关系的比较，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
17．椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1的焦点为F1、F2，点P在椭圆上，若|PF1|=3，则△PF1F2的面积为（ ）
| A． | $\sqrt{2}$ | B． | 2$\sqrt{2}$ | C． | 4$\sqrt{2}$ | D． | $\frac{9}{2}$ |
18．在数列{an}中，a1=1，若an-an-1=n-1（n∈N*，n≥2），则数列{an}的通项公式an=（ ）
| A． | $\frac{n（n+1）}{2}$ | B． | $\frac{{n}^{2}-n+2}{2}$ | C． | 2n2-n | D． | 2n-1 |
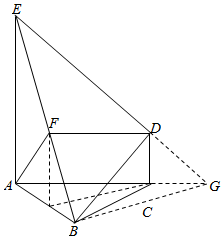如图所示，△ABC是正三角形，线段EA和DC都垂直于平面ABC，设EA=AB=2a，且F为的BE中点