题目内容

已知a，b，c∈R，a＞b＞c，且a+b+c=0．
（1）求证：a＞0；
（2）求证：ab+bc+ca＜0．
考点：不等式的证明
专题：不等式
分析：（1）利用反证法，即可证明，
（2）由题意得（a+b+c）2=0，即a2+b2+c2+2ab+2bc+2ca=0，问题的证明．
解答： 解：（反证法）假设a≤0，∵a＞b＞c，b＜0，c＜0
∴a+b+c＜0，与a+b+c=0矛盾，
∴假设不成立，
故a＞0，
（2）∵a+b+c=0．
∴（a+b+c）2=0，
∴a2+b2+c2+2ab+2bc+2ca=0，
即2ab+2bc+2ca=-（a2+b2+c2），
∴2ab+2bc+2ca＜0，
∴ab+bc+ca＜0．
点评：本题考查不等式的证明方法，以及反证法，属于基础题．
练习册系列答案
相关题目
设函数y=f（x）是定义域在R，并且满足f（x+y）=f（x）+f（y），f（
1
3
）=1，且当x＞0时，f（x）＜0．
（1）求f（0）的值；
（2）判断函数的奇偶性；
（3）如果f（x）+f（2+x）＜2，求x的取值范围．
已知cosα=
1
7
，cos（α+β）=-
11
14
，且α、β∈（0，
π
2
），求cosβ的值．
设两抛物线y=-x2+2x，y=x2所围成的图形为M，求：
（1）M的面积；
（2）将M绕x轴旋转一周所得旋转体的体积．
某市规定中学生百米成绩达标标准为不超过16秒．现从该市中学生中按照男、女生比例随机抽取了50人，其中有30人达标．将此样本的频率估计为总体的概率．
（1）随机调查45名学生，设ξ为达标人数，求ξ的数学期望与方差；
（2）如果男、女生采用相同的达标标准，男、女生达标情况如下表：
男女总计
达标a=24b=
 
 
不达标c=
 
d=12
 
总计
 
 
n=50
根据表中所给的数据，完成2×2列联表，并判断能否有99%的把握认为“体育达标与性别有关”？若有，你能否给出一个更合理的达标方案？
P（K2≥k0）0.0500.0100.001
k03.8416.63510.828
参考公式：K2=
n(ad-bc)2
(a+c)(b+d)(a+b)(c+d)
．
已知向量：
a
=（cosα，sinα），
b
=（cosβ，sinβ），且
a
，
b
满足关系|k
a
+
b
|=
3
|
a
-k
b
|（k为正实数）．
（1）求证：（
a
+
b
）⊥（
a
-
b
）；
（2）求证
a
与
b
的数量积表示为关于k的函数f（k）．
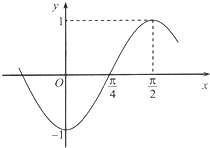已知函数f（x）=Asin（ωx+φ），（ω＞0，|φ|＜π）部分图象如图所示．
（1）求?，ϕ的值；
（2）若方程f（x+
π
3
）=m在区间[{0，
π
2
]内有两个不相等的实数根x1，x2．求：
i）m的取值范围；
ii）求x1+x2．
在生产过程中，测得纤维产品的纤度（表示纤维粗细的一种量）共有100个数据，将数据分组如右表：
分组频数
[1.30，1.34）4
[1.34，1.38）25
[1.38，1.42）30
[1.42，1.46）29
[1.46，1.50）10
[1.50，1.54）2
合计100
（1）画出频率分布表，并画出频率分布直方图；
（2）估计纤度落在[1.38，1.50）中的概率；
（3）从频率分布直方图估计出纤度的众数、中位数和平均数．
从0到9这10个数字中任取3个数字组成一个没有重复数字的三位数，能被3整除的数有
 
　个．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网