题目内容

已知p：实数x满足
0＜x≤4
x2-2x-1＞0
，q：实数x满足x2-4ax+3a2＜0（a＞0）
（1）当a=2，x=3时，试判断命题p∧q的真假
（2）若q是p的充分不必要条件，求实数a的取值范围．
考点：必要条件、充分条件与充要条件的判断,复合命题的真假
专题：简易逻辑
分析：（1）若a=2，x=3，分别求出p，q成立的等价条件，即可得到结论．
（2）若q是p的充分不必要条件，根据充分条件和必要条件的定义建立不等式关系即可求实数a的取值范围．
解答： 解：（1）当a=2，x=3时，
∵x=3满足不等式组
0＜x≤4
x2-2x-1＞0
，∴p是真命题；----------------------------（2分）
∵x=3也满足x2-8x+12＜0，∴q也是真命题．
∴p∧q是真命题．--------------------------------------（4分）
（2）由
0＜x≤4
x2-2x-1＞0
得1+
2
＜x≤4，-------------------------------------------（6分）
由x2-4ax+3a2＜0得a＜x＜3a，--------------------------------------（8分）
∵p是q的充分不必要条件，知(1+
2
，4]是（a，3a）的真子集，
∴
a≤1+
2
3a＞4
，---------------------------------------------------------------（10分）
得
4
3
＜a≤1+
2
-------------------------------------（11分）
∴实数a的取值范围为{a|
4
3
＜a≤1+
2
}----------------------------------------------（12分）
点评：本题主要考查基本逻辑用语，逻辑联结词以及充分必要条件，考查不等式解法及推理论证能力．
练习册系列答案
相关题目
函数y=|log 
3
4
x|的定义域为[m，n]（m＜n），值域为[0，1]，则n-m的最小值为（　　）
A、
3
4
B、
1
3
C、
1
4
D、
1
5
计算
416
+（-
27
8
） 
1
3
+log48的值是
 
．
化简
1-x
x
÷
1-x
x2
的结果为（　　）
A、x
B、-x
C、
1
x
D、-
1
x
△ABC的内角A，B，C的对边分别为a，b，c，若A，B，C成等差数列，a，b，c成等比数列，则sinA•sinC=
 
．
已知三点A（1，-1），B（a，3），C（4，5）在同一直线上，则实数a的值是（　　）
A、1B、3C、4D、不确定
设f（x）=
-2x+a
2x+1+b
（a＞0，b＞0），当a=b=1时，证明：f（x）不是奇函数．
函数y=ax+2014+2014（a＞0，且a≠1）的图象恒过定点（　　）
A、（0，1）
B、（0，2014）
C、（-2014，2015）
D、（-2014，2014）
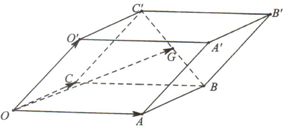如图，平行六面体OABC-O′A′B′C′中，设
OA
=
a
，
OC
=
b
，
OO′
=
c
，G为BC′的中点，用
a
，
b
，
c
表示向量
OG
，则
OG
等于（　　）
A、
a
+
1
2
b
+
1
2
c
B、
1
2
a
+
1
2
b
+
c
C、
1
2
a
+
b
+
1
2
c
D、
1
2
a
+
b
-
1
2
c

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网