Question

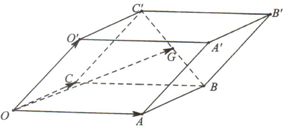如图，平行六面体OABC-O′A′B′C′中，设

OA

=

a

，

OC

=

b

，

OO′

=

c

，G为BC′的中点，用

a

，

b

，

c

表示向量

OG

，则

OG

等于（　　）

• A、

  a

  +

  1

  2

  b

  +

  1

  2

  c

• B、

  1

  2

  a

  +

  1

  2

  b

  +

  c

• C、

  1

  2

  a

  +

  b

  +

  1

  2

  c

• D、

  1

  2

  a

  +

  b

  -

  1

  2

  c

Answer 1

考点：平面向量的基本定理及其意义

专题：平面向量及应用

分析：根据向量的加法运算，向量加法的平行四边形法则，以及平行六面体的边的关系即可用

a

，

b

，

c

表示出

OG

．

解答： 解：

OG

=

OO′

+

O′C′

+

C′G

=

OO′

+

OC

+

1

2

(

OA

-

OO′

)=

1

2

a

+

b

+

1

2

c

．
故选C．

点评：考查向量的加法运算，向量加法的平行四边形法则，以及平行六面体边的关系，相等向量，相反向量的概念．