题目内容
20.函数f(x)=$\frac{x}{x+1}$+$\frac{x+1}{x+2}$+$\frac{x+2}{x+3}$的对称中心为(-2,3).分析 化简函数的解析式,根据函数的解析式可得它的图象的对称性.
解答 解:函数f(x)=$\frac{x}{x+1}$+$\frac{x+1}{x+2}$+$\frac{x+2}{x+3}$=1-$\frac{1}{x+1}$+1-$\frac{1}{x+2}$+1-$\frac{1}{x+3}$=3-($\frac{1}{x+1}$+$\frac{1}{x+2}$+$\frac{1}{x+3}$),
它的定义域为{x|x≠-1,x≠-2,x≠-3},$\frac{-1+(-3)}{2}$=-2.
又 f(-4-x)=3+($\frac{1}{x+1}$+$\frac{1}{x+2}$+$\frac{1}{x+3}$),∴f(x)+f(-4-x)=6,
故f(x)的图象的对称中心为(-2,3),
故答案为:(-2,3).
点评 本题主要考查函数的图象的对称性,考查转化思想以及计算能力,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
15.已知不等式组$\left\{\begin{array}{l}{x+y-4≤0}\\{x-4y+1≤0}\end{array}\right.$所表示的平面区域为M,不等式组$\left\{\begin{array}{l}{2x-3y-3≥0}\\{2x+2y-3≤0}\end{array}\right.$所表示的平面区域为N,若M中存在点在圆C:(x-3)2+(y-1)2=r2(r>0)内,但N中不存在点在圆C内.则r的取值范围是( )
| A. | (0,$\frac{\sqrt{13}}{2}$] | B. | ($\frac{\sqrt{13}}{2}$,$\sqrt{17}$) | C. | (0,$\sqrt{17}$) | D. | (0,$\frac{5\sqrt{2}}{4}$) |
12.在等比数列{an}中,如果a1+a2=40,a3+a4=60,那么a5+a6等于( )
| A. | 80 | B. | 90 | C. | 95 | D. | 100 |
9.已知向量$\overrightarrow{a}$=(2,1),向量$\overrightarrow{b}$=(3,-4),若向量$λ\overrightarrow{a}$-$\overrightarrow{b}$与向量$\overrightarrow{a}+2\overrightarrow{b}$是共线向量,则实数λ的取值为( )
| A. | -$\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{2}$ | D. | 2 |
15.经过圆x2+y2+2y=0的圆心且与直线x+2y-2=0平行的直线方程是( )
| A. | x+2y-1=0 | B. | x+2y+2=0 | C. | x+2y+1=0 | D. | x+2y+3=0 |
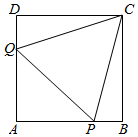 某地政府为提升城市形象,在该地区边长为1的正方形ABCD的空地建文化广场,在正方形ABCD的内部规划一块△CPQ区域种植花草,并满足P,Q分别为边AB,DA上的动点,且∠PCQ=$\frac{π}{3}$,问∠PCB多大时才能使△CPQ面积的最小,并求出最小值.
某地政府为提升城市形象,在该地区边长为1的正方形ABCD的空地建文化广场,在正方形ABCD的内部规划一块△CPQ区域种植花草,并满足P,Q分别为边AB,DA上的动点,且∠PCQ=$\frac{π}{3}$,问∠PCB多大时才能使△CPQ面积的最小,并求出最小值.