题目内容
10.在平行四边形中,AC与BD交于点O,$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{DO}$,CE的延长线与AD交于点F,若$\overrightarrow{CF}$=$λ\overrightarrow{AC}$+$μ\overrightarrow{BD}$(λ,μ∈R),则λ+μ=-$\frac{1}{3}$.分析 利用三角形的相似关系,求得$\overrightarrow{GF}$=$\frac{1}{3}$$\overrightarrow{BD}$,再根据向量的加法的三角形法则,求得λ和μ的值.
解答 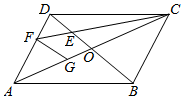 解:∵△FED∽△CEB,
解:∵△FED∽△CEB,
DF:CD=DE:EA=1:3,
过点F作FG∥BD交AC于G,
FG:DO=2:3,
AG:AO=2:3,
∴$\overrightarrow{GF}$=$\frac{1}{3}$$\overrightarrow{BD}$,
∵$\overrightarrow{CG}$=$\overrightarrow{CO}$+$\overrightarrow{OG}$=$\frac{2}{3}\overrightarrow{CA}$,
∴$\overrightarrow{CF}=\overrightarrow{AG}+\overrightarrow{GF}$=$\frac{2}{3}\overrightarrow{CA}$+$\frac{1}{3}$$\overrightarrow{BD}$,
$\overrightarrow{CF}$=$-\frac{2}{3}\overrightarrow{AC}+\frac{1}{3}\overrightarrow{BD}$,
λ+μ=-$\frac{1}{3}$.
故答案为:-$\frac{1}{3}$.
点评 本题考查根据三角形的相似关系,求得三角各边的比值,再根据向量加法的三角形法则,求得其和向量,属于中档题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
20.盒中共有6件除了颜色外完全相同的产品,其中有1件红色,2件白色和3件黑色,从中任取两件,则两件颜色不相同的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{7}{15}$ | C. | $\frac{3}{5}$ | D. | $\frac{11}{15}$ |
1.大学生甲、乙、丙为唐山世园会的两个景区提供翻译服务,每个景区安排一名或两名大学生,则甲、乙被安排到不同景区的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{6}$ | D. | $\frac{2}{3}$ |
19.某市甲、乙、丙3个区的高中学生人数之比为2:3:5,现要用分层抽样方法从该市甲、乙、丙3个区所有高中学生中抽取一个样本,已知从甲区中抽取了80人,则应从乙、丙2个区中共抽取( )
| A. | 120人 | B. | 200人 | C. | 320人 | D. | 400人 |