题目内容
9.已知向量$\overrightarrow{a}$=(2,1),向量$\overrightarrow{b}$=(3,-4),若向量$λ\overrightarrow{a}$-$\overrightarrow{b}$与向量$\overrightarrow{a}+2\overrightarrow{b}$是共线向量,则实数λ的取值为( )| A. | -$\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{2}$ | D. | 2 |
分析 先求出$λ\overrightarrow{a}-\overrightarrow{b}$=(2λ-3,λ+4),$\overrightarrow{a}+2\overrightarrow{b}$=(8,-7),再由向量$λ\overrightarrow{a}$-$\overrightarrow{b}$与向量$\overrightarrow{a}+2\overrightarrow{b}$是共线向量,能求出实数λ的取值.
解答 解:∵向量$\overrightarrow{a}$=(2,1),向量$\overrightarrow{b}$=(3,-4),
∴$λ\overrightarrow{a}-\overrightarrow{b}$=(2λ-3,λ+4),$\overrightarrow{a}+2\overrightarrow{b}$=(8,-7),
∵向量$λ\overrightarrow{a}$-$\overrightarrow{b}$与向量$\overrightarrow{a}+2\overrightarrow{b}$是共线向量,
∴$\frac{2λ-3}{8}=\frac{λ+4}{-7}$,
解得$λ=-\frac{1}{2}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意向量共线的条件的合理运用.

练习册系列答案
相关题目
19.某市甲、乙、丙3个区的高中学生人数之比为2:3:5,现要用分层抽样方法从该市甲、乙、丙3个区所有高中学生中抽取一个样本,已知从甲区中抽取了80人,则应从乙、丙2个区中共抽取( )
| A. | 120人 | B. | 200人 | C. | 320人 | D. | 400人 |
17.如果实数x,y,满足条件$\left\{\begin{array}{l}{x-y+1≥0}\\{2x+y-2≥0}\\{x-1≤0}\end{array}\right.$,则z=1-$\frac{2}{2x+3y}$的最大值为( )
| A. | 1 | B. | $\frac{3}{4}$ | C. | 0 | D. | $\frac{4}{7}$ |
4.已知集合A={-2,3},B={x|lnx>1},则A∩B=( )
| A. | {-2} | B. | {3} | C. | {-2,3} | D. | ∅ |
14.已知角α的顶点在原点,始边与Ox轴重合,终边经过(4a,3a)(a<0),则下列计算正确的是( )
| A. | sinα=$\frac{3}{5}$ | B. | cosα=$\frac{4}{5}$ | C. | tanα=-$\frac{3}{4}$ | D. | sinα=-$\frac{3}{5}$ |
3. 某市四所重点中学进行高二期中联考,共有5000名学生参加,为了了解数学学科的学习情况,现从中随机的抽取若干名学生在这次测试中的数学成绩,制成如下频率分布表:
某市四所重点中学进行高二期中联考,共有5000名学生参加,为了了解数学学科的学习情况,现从中随机的抽取若干名学生在这次测试中的数学成绩,制成如下频率分布表:
(1)根据上面的频率分布表,推出①,②,③,④处的数字分别为,3,0.025,0.1,1;
(2)在所给的坐标系中画出[80,150]上的频率分布直方图;
(3)根据题中的信息估计总体:
①120分及以上的学生人数;
②成绩在[126,150]中的概率.
 某市四所重点中学进行高二期中联考,共有5000名学生参加,为了了解数学学科的学习情况,现从中随机的抽取若干名学生在这次测试中的数学成绩,制成如下频率分布表:
某市四所重点中学进行高二期中联考,共有5000名学生参加,为了了解数学学科的学习情况,现从中随机的抽取若干名学生在这次测试中的数学成绩,制成如下频率分布表:| 分组 | 频数 | 频率 |
| [80,90) | ① | ② |
| [90,100) | 0.050 | |
| [100,110) | 0.200 | |
| [110,120) | 36 | 0.300 |
| [120,130) | 0.275 | |
| [130,140) | 12 | ③ |
| [140,150] | 0.050 | |
| 合计 | ④ |
(2)在所给的坐标系中画出[80,150]上的频率分布直方图;
(3)根据题中的信息估计总体:
①120分及以上的学生人数;
②成绩在[126,150]中的概率.
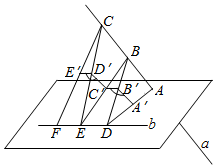 如图,直线a,b是异面直线,A,B,C为直线a上三点,D,E,F是直线b上三点,A′,B′,C′,D′,E′分别为AD,DB,BE,EC,CF的中点.
如图,直线a,b是异面直线,A,B,C为直线a上三点,D,E,F是直线b上三点,A′,B′,C′,D′,E′分别为AD,DB,BE,EC,CF的中点.