题目内容
4.已知$f(x)=\left\{\begin{array}{l}1-{x^2},\;x≤1\\ mlnx,\;x>1\end{array}\right.$,若函数y=f(x)-x恰有三个零点,则f(m)=e.分析 判断函数函数y=f(x)-x,x≤1时,零点个数,然后判断x>1时零点个数,转化求解即可.
解答 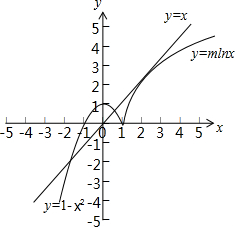 解:$f(x)=\left\{\begin{array}{l}1-{x^2},\;x≤1\\ mlnx,\;x>1\end{array}\right.$,
解:$f(x)=\left\{\begin{array}{l}1-{x^2},\;x≤1\\ mlnx,\;x>1\end{array}\right.$,
若函数y=f(x)-x恰有三个零点,
在平面直角坐标系画出y=f(x)与y=x的图象,
如图:
当x≤1时,零点有2个数,当x>1时零点个数为1个,
y=mlnx与y=x只有一个交点,可得y′=$\frac{m}{x}$,切点坐标想,(x,x),
可得m=x,可得x=xlnx,解得x=m=e.
f(m)=elne=e.
故答案为:e.
点评 本题考查函数的导数的应用,函数的零点的求法,考查数形结合以及转化思想的应用.

练习册系列答案
相关题目
19.在△ABC中,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{BD}=2\overrightarrow{DC}$,则$\overrightarrow{AD}•\overrightarrow{BC}$的值为( )
| A. | $-\frac{1}{3}$ | B. | $-\frac{2}{3}$ | C. | -1 | D. | $-\frac{4}{3}$ |
16.已知x,y满足约束条件$\left\{{\begin{array}{l}{3x-y≤0}\\{2y-3x-6≤0}\\ \begin{array}{l}x≥0\\ y≥0\end{array}\end{array}}\right.$,则$z=\frac{2^x}{{\sqrt{2^y}}}$的最小值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 1 | D. | ${2^{-\frac{3}{2}}}$ |
13.已知$f(\sqrt{x})=x$,则函数f(x+2)为( )
| A. | y=x2+4x+4(x≥-2) | B. | y=x2-4x+4(x≥0) | C. | y=x2+2(x≥0) | D. | y=x2-2(x≥0) |