题目内容
11.设集合A={y|y=x2+2x-1,x∈R},B={x|x2-1≤0},则A∩B=( )| A. | [-2,+∞) | B. | [-1,+∞) | C. | [-1,1] | D. | [-2,1] |
分析 先分别求出集合A和B,由此利用交集定义能求出结果.
解答 解:∵集合A={y|y=x2+2x-1,x∈R}
={y|y=(x+1)2-2}={y|y≥-2},
B={x|x2-1≤0}={x|-1≤x≤1},
∴A∩B=[-1,1].
故选:C.
点评 本题考查交集的求法,是基础题,解题时要认真审题,注意交集定义的合理运用.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
1.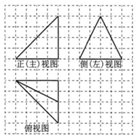 在正方形网格中,某四面体的三视图如图所示.如果小正方形网格的边长为1,那么该四面体最长棱的棱长为( )
在正方形网格中,某四面体的三视图如图所示.如果小正方形网格的边长为1,那么该四面体最长棱的棱长为( )
 在正方形网格中,某四面体的三视图如图所示.如果小正方形网格的边长为1,那么该四面体最长棱的棱长为( )
在正方形网格中,某四面体的三视图如图所示.如果小正方形网格的边长为1,那么该四面体最长棱的棱长为( )| A. | 4$\sqrt{3}$ | B. | 6 | C. | 4$\sqrt{2}$ | D. | 2$\sqrt{5}$ |
19.下列各数中,是纯虚数的是( )
| A. | i2 | B. | π | C. | 1+$\sqrt{3}$i | D. | (1+$\sqrt{3}$)i |
16.若点P是以F1,F2为焦点的双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)上一点,PF1⊥PF2,且|PF1|=2|PF2|,则此双曲线的标准方程是( )
| A. | x2-$\frac{{y}^{2}}{4}$=1 | B. | x2-$\frac{{y}^{2}}{3}$=1 | C. | x2-$\frac{{y}^{2}}{5}$=1 | D. | x2-$\frac{{y}^{2}}{6}$=1 |
20.已知f(x)=x3-ax在(-∞,-1]上是单调函数,则a的取值范围是( )
| A. | (3,+∞) | B. | [3,+∞) | C. | (-∞,3) | D. | (-∞,3] |
1.已知函数f(x)=|lnx|,若f(m)=f(n)(m>n>0),则$\frac{2}{m+1}$+$\frac{2}{n+1}$=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |