题目内容
20.设数列{an}的前n项和为Sn,且Sn=3an+2.(1)求数列{an}的通项公式;
(2)求数列{nan}的前n项和Tn.
分析 (1)利用递推关系与等比数列的通项公式即可得出.
(2)nan=-n$(\frac{3}{2})^{n-1}$.再利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:(1)∵Sn=3an+2,∴当n=1时,a1=3a1+2,解得a1=-1.
当n≥2时,an=Sn-Sn-1=(3an+2)-(3an-1+2),化为${a}_{n}=\frac{3}{2}{a}_{n-1}$,
∴数列{an}是等比数列,首项为-1,公比为$\frac{3}{2}$,解得an=-$(\frac{3}{2})^{n-1}$.
(2)nan=-n$(\frac{3}{2})^{n-1}$.
∴数列{nan}的前n项和Tn=-1-$2×\frac{3}{2}$-3×$(\frac{3}{2})^{2}$-…-$n×(\frac{3}{2})^{n-1}$,
即-Tn=1+$2×\frac{3}{2}$+3×$(\frac{3}{2})^{2}$+…+$n×(\frac{3}{2})^{n-1}$,
$-\frac{3}{2}{T}_{n}$=$\frac{3}{2}$+2×$(\frac{3}{2})^{2}$+…+(n-1)×$(\frac{3}{2})^{n-1}$+n×$(\frac{3}{2})^{n}$,
∴$\frac{1}{2}{T}_{n}$=1+$\frac{3}{2}$+$(\frac{3}{2})^{2}$+…+$(\frac{3}{2})^{n-1}$-n×$(\frac{3}{2})^{n}$=$\frac{(\frac{3}{2})^{n}-1}{\frac{3}{2}-1}$-n×$(\frac{3}{2})^{n}$=$(2-n)×(\frac{3}{2})^{n}$-2,
∴Tn=$(4-2n)×(\frac{3}{2})^{n}$-4.
点评 本题考查了递推关系、等比数列的通项公式与前n项和公式、“错位相减法”,考查了推理能力与计算能力,属于中档题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | a是整数 | B. | a是无理数 | C. | a是有理数 | D. | a不存在 |
| A. | x2+$\frac{8}{7}$x+1 | B. | $\frac{2}{7}$x2+x+1 | C. | $\frac{2}{7}$x2+$\frac{8}{7}$x | D. | $\frac{2}{7}$x2+$\frac{8}{7}$x+1 |
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
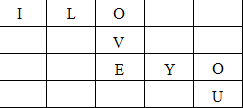 将“I LOVE YOU”8个英文字母填入5×4的方格中,其中“I“字母填入左上角,“U”字母填入右下角,将其余6个英文字母依次填入方格,要求只能横读或竖读成一句原话,如图所示为一种填法,则共有35种不同的填法.(用数字作答)
将“I LOVE YOU”8个英文字母填入5×4的方格中,其中“I“字母填入左上角,“U”字母填入右下角,将其余6个英文字母依次填入方格,要求只能横读或竖读成一句原话,如图所示为一种填法,则共有35种不同的填法.(用数字作答)