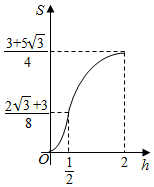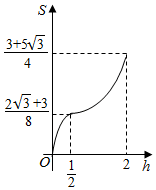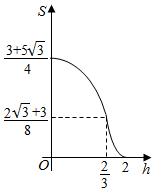题目内容
14．若复数Z满足（1+i）Z=|3+4i|，则Z的实部为（ ）| A． | -$\frac{3}{2}$ | B． | -$\frac{5}{2}$ | C． | $\frac{3}{2}$ | D． | $\frac{5}{2}$ |
分析 把已知等式变形，求出分子的模，再利用复数代数形式的乘除运算化简得答案．
解答 解：由（1+i）Z=|3+4i|，得$Z=\frac{|3+4i|}{1+i}=\frac{\sqrt{{3}^{2}+{4}^{2}}}{1+i}=\frac{5（1-i）}{（1+i）（1-i）}=\frac{5}{2}-\frac{5}{2}i$，
∴Z的实部为$\frac{5}{2}$．
故选：D．
点评 本题考查复数代数形式的乘除运算，考查了复数模的求法，是基础题．
练习册系列答案
相关题目
4．设函数f（x）=$\left\{\begin{array}{l}cosπx，x＞0\\ f（x+1）-1，x≤0\end{array}$，则f（-$\frac{4}{3}$）的值为（ ）
| A． | $-\frac{3}{2}$ | B． | $\frac{{\sqrt{3}}}{2}-2$ | C． | $-\frac{{\sqrt{3}}}{2}-2$ | D． | $-\frac{5}{2}$ |
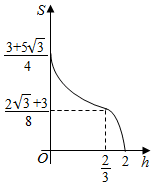
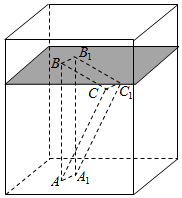已知三棱柱ABC-A1B1C1，侧棱BB1⊥平面ABC，AB=2，AC=$\sqrt{3}$，AA1=$\frac{1}{4}$，AC⊥BC，将其放入一个水平放置的水槽中，使AA1在水槽底面内，平面ABB1A1与水槽底面垂直，且水面恰好经过棱BB1，现水槽底面出现一个洞，水位下降，则在水位下降过程中，几何体露出水面部分的面积S关于水位下降的高度h的图象大致为（ ）
19．已知函数$f（x）=\left\{\begin{array}{l}{log_5}x，x＞0\\{2^x}\;\;，x≤0\end{array}\right.$，则$f（f（\frac{1}{25}））$=（ ）
| A． | 4 | B． | $\frac{1}{4}$ | C． | -4 | D． | $-\frac{1}{4}$ |
6．设复数z1，z2在复平面内对应的点关于虚轴对称，且z1=2+i，则z2=（ ）
| A． | 2+i | B． | -2+i | C． | 2-i | D． | -2-i |