题目内容
19．已知函数$f（x）=\left\{\begin{array}{l}{log_5}x，x＞0\\{2^x}\;\;，x≤0\end{array}\right.$，则$f（f（\frac{1}{25}））$=（ ）| A． | 4 | B． | $\frac{1}{4}$ | C． | -4 | D． | $-\frac{1}{4}$ |
分析 由分段函数及复合函数知，从内向外依次代入求值即可．
解答 解：f（$\frac{1}{25}$）=log5$\frac{1}{25}$=-2，
$f（f（\frac{1}{25}））$=f（-2）=$\frac{1}{4}$，
故选：B．
点评 本题考查了分段函数与复合函数的应用及学生的化简运算能力的应用．
练习册系列答案
相关题目
10．函数f（x）=Acos（ωx+φ）在区间[0，π]上的图象如图所示，则函数f（x）的解析式可能是（ ）
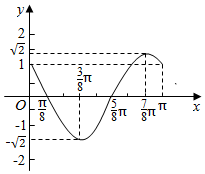
| A． | f（x）=2cos（2x+$\frac{π}{4}$） | B． | f（x）=-$\sqrt{2}$cos（x-$\frac{π}{4}$） | C． | f（x）=-$\sqrt{2}$cos（2x-$\frac{3π}{4}$） | D． | f（x）=$\sqrt{2}$cos（2x-$\frac{π}{4}$） |
7．若存在实数x，y满足$\left\{\begin{array}{l}{2x-y-2＜0}\\{x-2y+2＞0}\\{x+y-2＞0}\\{m（x+1）-y=0}\\{\;}\end{array}\right.$，则实数m的取值范围是（ ）
| A． | （0，$\frac{2}{7}$） | B． | （$\frac{2}{7}$，$\frac{2}{3}$） | C． | （$\frac{2}{3}$，$\frac{4}{5}$） | D． | （$\frac{2}{7}$，$\frac{4}{5}$） |
14．若复数Z满足（1+i）Z=|3+4i|，则Z的实部为（ ）
| A． | -$\frac{3}{2}$ | B． | -$\frac{5}{2}$ | C． | $\frac{3}{2}$ | D． | $\frac{5}{2}$ |
9．在△ABC中，∠BAC=75°，AB=3，AC=4，若点D，E都在边BC上，并且∠BAD=∠CAE=30°，则$\frac{BD•BE}{CD•CE}$=（ ）
| A． | $\frac{\sqrt{6}}{4}$ | B． | $\frac{3}{4}$ | C． | $\frac{9}{16}$ | D． | $\sqrt{2}$ |