题目内容
7.已知变量x,y满足约束条件$\left\{\begin{array}{l}{x+y-2≥0}\\{2x-y-1≤0}\\{x+4y-14≤0}\end{array}\right.$,则z=$\frac{y+2}{x+1}$的取值范围是$(-∞,-6]∪[\frac{3}{2},+∞)$.分析 由约束条件作出可行域,利用z=$\frac{y+2}{x+1}$的几何意义结合两点连线的斜率得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x+y-2≥0}\\{2x-y-1≤0}\\{x+4y-14≤0}\end{array}\right.$作出可行域如图,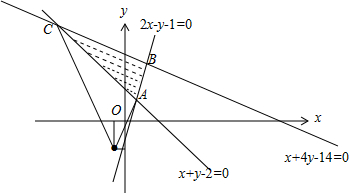
联立$\left\{\begin{array}{l}{x+y-2=0}\\{2x-y-1=0}\end{array}\right.$,解得:A(1,1),
联立$\left\{\begin{array}{l}{x+y-2=0}\\{x+4y-14=0}\end{array}\right.$,解得C(-2,4),
z=$\frac{y+2}{x+1}$的几何意义是可行域内的动点与定点P(-1,-2)连线的斜率,
∵${k}_{PA}=\frac{-2-1}{-1-1}=\frac{3}{2}$,${k}_{PC}=\frac{4+2}{-2+1}=-6$.
∴z=$\frac{y+2}{x+1}$的取值范围是$(-∞,-6]∪[\frac{3}{2},+∞)$.
故答案为:$(-∞,-6]∪[\frac{3}{2},+∞)$.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,考查了数学转化思想方法,是中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
16.已知△ABC的三个顶点在以O为球心的球面上,且cosC=$\frac{1}{3}$,BC=1,AC=3,三棱锥O-ABC的体积为$\frac{\sqrt{14}}{6}$,则球O的表面积为( )
| A. | 4π | B. | 8π | C. | 16π | D. | 24π |
12.设抛物线C:y=x2与直线l:y=1围成的封闭图形记为P,则图形P的面积S等于( )
| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
15.已知函数f(x)=ln(x+1)-ax的图象在x=1处的切线与直线x+2y-1=0平行,且方程f(x)=$\frac{1}{4}$(m-3x)在[2,4]上有两个不相等的实数根,则实数m的取值范围为( )
| A. | (4ln5-4,4ln4-3) | B. | [4ln3-2,4ln5-4] | C. | [4ln3-2,4ln4-3] | D. | [4ln5-4,4ln4-3) |
15.下列命题中,真命题的是( )
| A. | ?x0∈R,ex0≤0 | B. | ?x∈R,2x>x2 | ||
| C. | “若x>3,则x>2”的否命题 | D. | “x2≠1”是“x≠1”的充分不必要条件 |
 的图象在
的图象在 上恰有两个点的纵坐标为
上恰有两个点的纵坐标为 ,则实数
,则实数 的取值范围是 .
的取值范围是 . 中,
中, ,且数列
,且数列 是等比数列,则
是等比数列,则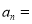 ___________.
___________.