题目内容
12.设抛物线C:y=x2与直线l:y=1围成的封闭图形记为P,则图形P的面积S等于( )| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
分析 由题意画出图形,把阴影部分的面积转化为长方形的面积与2${∫}_{0}^{1}{x}^{2}dx$的差得答案.
解答 解:如图,
S=1×2-2${∫}_{0}^{1}{x}^{2}dx$=2-2×$\frac{1}{3}{x}^{3}{|}_{0}^{1}$=2-$\frac{2}{3}$=$\frac{4}{3}$.
故选:D.
点评 本题考查了定积分,考查了数形结合的解题思想方法,是基础题.

练习册系列答案
相关题目
17.定义域为R的偶函数f(x)满足对任意x∈R,有f(x+2)=f(x)-f(1),且当x∈[2,3]时,f(x)=-2x2+12x-18,若函数y=f(x)-loga(x+1)在(0,+∞)上恰有三个零点,则a的取值范围是( )
| A. | (0,$\frac{{\sqrt{2}}}{2}$) | B. | (0,$\frac{{\sqrt{3}}}{3}$) | C. | (0,$\frac{{\sqrt{5}}}{5}$) | D. | ($\frac{{\sqrt{5}}}{5}$,$\frac{{\sqrt{3}}}{3}$) |
3.已知点(x,y)满足$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≤1}\end{array}\right.$,则u=y-x的最小值是( )
| A. | 1 | B. | -2 | C. | 0 | D. | -1 |
20.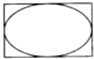 如图所示,矩形长为6,宽为4,在矩形内随机的撒2400颗黄豆,数得落在椭圆外的黄豆数为516颗,依据此实验数据可以估计出椭圆的面积约为( )
如图所示,矩形长为6,宽为4,在矩形内随机的撒2400颗黄豆,数得落在椭圆外的黄豆数为516颗,依据此实验数据可以估计出椭圆的面积约为( )
 如图所示,矩形长为6,宽为4,在矩形内随机的撒2400颗黄豆,数得落在椭圆外的黄豆数为516颗,依据此实验数据可以估计出椭圆的面积约为( )
如图所示,矩形长为6,宽为4,在矩形内随机的撒2400颗黄豆,数得落在椭圆外的黄豆数为516颗,依据此实验数据可以估计出椭圆的面积约为( )| A. | 17.84 | B. | 18.84 | C. | 5.16 | D. | 6.16 |
 分别与曲线
分别与曲线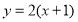 ,
, 交于A,B,则
交于A,B,则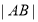 的最小值为( )
的最小值为( ) D.
D.