题目内容
15.已知函数f(x)=ln(x+1)-ax的图象在x=1处的切线与直线x+2y-1=0平行,且方程f(x)=$\frac{1}{4}$(m-3x)在[2,4]上有两个不相等的实数根,则实数m的取值范围为( )| A. | (4ln5-4,4ln4-3) | B. | [4ln3-2,4ln5-4] | C. | [4ln3-2,4ln4-3] | D. | [4ln5-4,4ln4-3) |
分析 由函数f(x)=ln(1+x)-ax的图象在x=1处的切线与直线x+2y-1=0平行,则在x=1处的导数等于直线x+2y-1=0的斜率,从而可得a=1.方程f(x)=$\frac{1}{4}$(m-3x)整理为4ln(1+x)-x=m.再利用图象的交点来解决.
解答 解:∵f′(x)=$\frac{1}{x+1}$-a,则f(x)的图象在x=1处的切线斜率为f′(1)=$\frac{1}{2}$-a,
由于切线与直线x+2y-1=0平行,
则f′(1)=$\frac{1}{2}$-a=-$\frac{1}{2}$,
解得a=1.
有f(x)=ln(1+x)-x,
∴原方程可整理为4ln(1+x)-x=m.
令g(x)=4ln(1+x)-x,得g′(x)=$\frac{4}{x+1}$-1,
∴当3<x≤4时g'(x)<0,当2≤x<3时g'(x)>0,g'(3)=0,
即g(x)在[2,3]上是增函数,在[3,4]上是减函数,
∴在x=3时g(x)有最大值4ln4-3.
∵g(2)=4ln3-2,g(4)=4ln5-4,
∴g(2)-g(4)=4ln$\frac{3}{5}$+2=2(2ln$\frac{3}{5}$+1).
由9e≈24.46<25,于是2ln$\frac{9e}{25}$<0.
∴g(2)<g(4).
∴m的取值范围为[4ln5-4,4ln4-3).
故选D.
点评 本题主要考查导数的运用:求切线的斜率和单调区间、极值和最值,用导数法解决方程根的问题,考查分离参数和构造函数的能力,属于中档题.

练习册系列答案
相关题目
7.已知抛物线y2=mx的焦点坐标为(2,0),则m的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | 4 | D. | 8 |
3.已知点(x,y)满足$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≤1}\end{array}\right.$,则u=y-x的最小值是( )
| A. | 1 | B. | -2 | C. | 0 | D. | -1 |
10.集合U={0,1,2,3,4},A={1,2},B={x∈Z|x2-5x+4<0},则∁U(A∪B)=( )
| A. | {0,1,3,4} | B. | {1,2,3} | C. | {0,4} | D. | {0} |
20.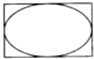 如图所示,矩形长为6,宽为4,在矩形内随机的撒2400颗黄豆,数得落在椭圆外的黄豆数为516颗,依据此实验数据可以估计出椭圆的面积约为( )
如图所示,矩形长为6,宽为4,在矩形内随机的撒2400颗黄豆,数得落在椭圆外的黄豆数为516颗,依据此实验数据可以估计出椭圆的面积约为( )
 如图所示,矩形长为6,宽为4,在矩形内随机的撒2400颗黄豆,数得落在椭圆外的黄豆数为516颗,依据此实验数据可以估计出椭圆的面积约为( )
如图所示,矩形长为6,宽为4,在矩形内随机的撒2400颗黄豆,数得落在椭圆外的黄豆数为516颗,依据此实验数据可以估计出椭圆的面积约为( )| A. | 17.84 | B. | 18.84 | C. | 5.16 | D. | 6.16 |
7.设Sn为等差数列{an}前项和,S6=3a3,a6=-2,则a8=( )
| A. | -6 | B. | -2 | C. | -4 | D. | 2 |