题目内容
已知在数列{an}中,Sn=4an+2,a1=-
,求数列{an}的通项公式.
| 2 |
| 3 |
考点:数列递推式
专题:等差数列与等比数列
分析:由已知得n≥2时,an=Sn-Sn-1=4an-4an-1,由此得到{an}是首项为-
,公比为
的等比数列,从而得到an=(-
)•(
)n-1.
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
解答:
解:∵Sn=4an+2,a1=-
,
∴n≥2时,an=Sn-Sn-1=4an-4an-1,
∴an=
an-1,
∴{an}是首项为-
,公比为
的等比数列,
∴an=(-
)•(
)n-1.
| 2 |
| 3 |
∴n≥2时,an=Sn-Sn-1=4an-4an-1,
∴an=
| 4 |
| 3 |
∴{an}是首项为-
| 2 |
| 3 |
| 4 |
| 3 |
∴an=(-
| 2 |
| 3 |
| 4 |
| 3 |
点评:本题考查数列的通项公式的求法,是中档题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
sin450°的值为( )
| A、-1 | ||
| B、0 | ||
C、
| ||
| D、1 |
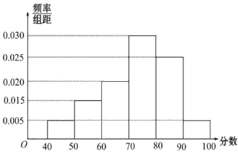 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.