题目内容
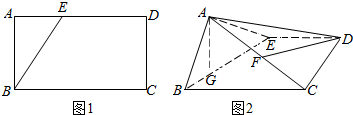
12.已知向量$\overrightarrow{OA}$、$\overrightarrow{OB}$(O、A、B三点不共线),求作下列向量:(1)$\overrightarrow{OM}$=$\frac{1}{2}$($\overrightarrow{OA}$+$\overrightarrow{OB}$);
(2)$\overrightarrow{ON}$=$\frac{1}{2}$($\overrightarrow{OA}$-$\overrightarrow{OB}$);
(3)$\overrightarrow{OG}$=3$\overrightarrow{OA}$+2$\overrightarrow{OB}$.
分析 利用向量加法和向量减法的平行四边形法则,及数乘向量的几何意义,可得相应的向量.
解答 解:(1)$\overrightarrow{OM}$=$\frac{1}{2}$($\overrightarrow{OA}$+$\overrightarrow{OB}$)如下图所示:
(2)$\overrightarrow{ON}$=$\frac{1}{2}$($\overrightarrow{OA}$-$\overrightarrow{OB}$)如下图所示:
(3)$\overrightarrow{OG}$=3$\overrightarrow{OA}$+2$\overrightarrow{OB}$如下图所示:
点评 本题考查的知识点是向量加减运算及数乘运算的几何意义,向量加法和向量减法的平行四边形法则,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.已知集合A={x∈Z|(x+1)(x-2)≤0},B={x|-2<x<2},则A∩B=( )
| A. | {x|-1≤x<2} | B. | {-1,0,1} | C. | {0,1,2} | D. | {-1,1} |
3.1和9的等比中项是( )
| A. | 5 | B. | 3 | C. | -3 | D. | ±3 |
 如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于N,过N 点的切线交C A 的延长线于P
如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于N,过N 点的切线交C A 的延长线于P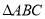 中,
中, 是
是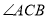 的角平分线,
的角平分线,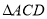 的外接圆交
的外接圆交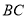 于
于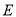 点.
点.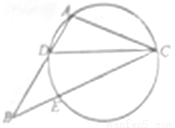
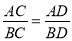 ;
;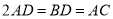 ,求
,求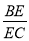 的值.
的值.