题目内容
17. 如图,已知DC⊥平面ABC,BE∥CD,是正三角形,AC=CD=2BE,且点M是AD上的一个动点.
如图,已知DC⊥平面ABC,BE∥CD,是正三角形,AC=CD=2BE,且点M是AD上的一个动点.(1)若点M是AD的中点,求证:ME∥平面ABC;
(2)求证:平面ADE⊥平面ACD.
分析 (1)取AC中点为F,连接BF,证明四边形MEBF是平行四边形,可得ME∥BF,即可证明ME∥平面ABC;
(2)证明ME⊥平面ACD,即可证明平面ADE⊥平面ACD.
解答 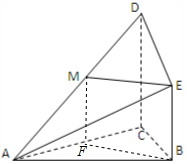 证明:(1)取AC中点为F,连接BF.
证明:(1)取AC中点为F,连接BF.
∵AM=MD,AF=FC,∴MF平行且等于$\frac{1}{2}$DC.
∵BE平行且等于$\frac{1}{2}$DC,∴BE平行且等于MF,
∴四边形MEBF是平行四边形,
∴ME∥BF.
∵ME?平面ABC,BF?平面ABC,
∴ME∥平面ABC;(6分)
(2)∵AF=CF,AB=CB,∴BF⊥AC.
∵DC⊥平面ABC,BF?平面ABC,∴DC⊥BF.
∵DC∩AC=C,∴BF⊥平面ACD.
由(1)中证明可知,ME∥BF.
∴ME⊥平面ACD,
∵ME?平面ADE,
∴平面ADE⊥平面ACD.…(12分)
点评 本题考查空间直线和平面的位置关系,考查空间想象能力、转化、论证能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.对部分4G手机用户每日使用流量(单位:M)进行统计,得到如下记录:
将手机日使用的流量统计到各组的频率视为概率,并假设每天手机的日流量相互独立.
(Ⅰ)求某人在未来连续4天里,有连续3天的手机的日使用流量都不低于15M且另1天的手机日使用流量低于5M的概率;
(Ⅱ)用X表示某人在未来3天时间里手机日使用流量不低于15M的天数,求X的分布列和数学期望.
| 流量x | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
| 频率 | 0.05 | 0.25 | 0.30 | 0.25 | 0.15 | 0 |
(Ⅰ)求某人在未来连续4天里,有连续3天的手机的日使用流量都不低于15M且另1天的手机日使用流量低于5M的概率;
(Ⅱ)用X表示某人在未来3天时间里手机日使用流量不低于15M的天数,求X的分布列和数学期望.
 的值域为
的值域为 ,则实数
,则实数 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
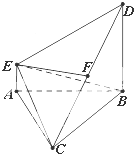 如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,2AE=BD=2.
如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,2AE=BD=2.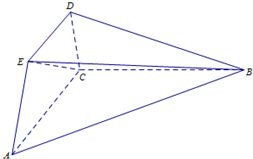 如图,已知平面ABC⊥平面ACDE,且△ABC为等腰直角三角形,AC=BC=4,等腰梯形ACDE中,AC∥DE且AE=DE=2.
如图,已知平面ABC⊥平面ACDE,且△ABC为等腰直角三角形,AC=BC=4,等腰梯形ACDE中,AC∥DE且AE=DE=2.