题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为
,点F1,F2分别是椭圆C的左,右焦点,以原点为圆心,椭圆C的短半轴为半径的圆与直线x-y+
=0相切.
(1)求椭圆C的方程;
(2)若过点F2的直线l与椭圆C相交于M,N两点,求△F1MN的内切圆面积的最大值和此时直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 6 |
(1)求椭圆C的方程;
(2)若过点F2的直线l与椭圆C相交于M,N两点,求△F1MN的内切圆面积的最大值和此时直线l的方程.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)利用椭圆C:
+
=1(a>b>0)的离心率为
,可得e=
=
,椭圆C的短半轴为半径的圆与直线x-y+
=0相切,求得a,b的值,则椭圆方程可求;
(2)设出直线l的方程x=my+1,和椭圆方程联立,得到当S△F1MN最大时,r也最大,△MF1N的内切圆面积也最大,利用根与系数关系把△MF1N的面积转化为含有m的代数式,利用基本不等式求得最值并得到直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| c |
| a |
| 1 |
| 2 |
| 6 |
(2)设出直线l的方程x=my+1,和椭圆方程联立,得到当S△F1MN最大时,r也最大,△MF1N的内切圆面积也最大,利用根与系数关系把△MF1N的面积转化为含有m的代数式,利用基本不等式求得最值并得到直线l的方程.
解答:
解:(1)∵椭圆C:
+
=1(a>b>0)的离心率为
,∴e=
=
,
∵椭圆C的短半轴为半径的圆与直线x-y+
=0相切.
∴b=
=
,
∴a=2,
∴椭圆C的方程为
+
=1;
(2)设直线l的方程为:x=my+1,代入椭圆方程可得(3m2+4)y2+6my-9=0.
△=(6m)2+36(3m2+4)=144m2+144>0.
设M(x1,y1),N(x2,y2),
∴y1+y2=-
,y1y2=-
,
∴S△F1MN=
|F1F2||y1-y2|=
=
≤3(m=0时取等号),
△MF1N的内切圆半径为r,则S△F1MN=
(|MN|+|F1M|+|F1N|)r=4r,
∴rmax=
,
这时△MF1N的内切圆面积的最大值为
π,直线l的方程为x=1.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| c |
| a |
| 1 |
| 2 |
∵椭圆C的短半轴为半径的圆与直线x-y+
| 6 |
∴b=
| ||
|
| 3 |
∴a=2,
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设直线l的方程为:x=my+1,代入椭圆方程可得(3m2+4)y2+6my-9=0.
△=(6m)2+36(3m2+4)=144m2+144>0.
设M(x1,y1),N(x2,y2),
∴y1+y2=-
| 6m |
| 3m2+4 |
| 9 |
| 3m2+4 |
∴S△F1MN=
| 1 |
| 2 |
12
| ||
| 3m2+4 |
| 12 | ||||||
3
|
△MF1N的内切圆半径为r,则S△F1MN=
| 1 |
| 2 |
∴rmax=
| 3 |
| 4 |
这时△MF1N的内切圆面积的最大值为
| 9 |
| 16 |
点评:本题考查了椭圆方程的求法,考查了直线与圆锥曲线的关系,直线与曲线联立,根据方程的根与系数的关系解题,是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考试具备较强的运算推理的能力,是压轴题.

练习册系列答案
相关题目
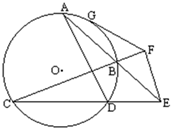 延长图O的两弦AB,CD交于圆外一点E,过E点作DA的平行线交CB的廷长线于点F,自F点作图0的切线FG.求证FG=FE.
延长图O的两弦AB,CD交于圆外一点E,过E点作DA的平行线交CB的廷长线于点F,自F点作图0的切线FG.求证FG=FE.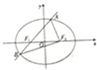 如图,椭圆E:
如图,椭圆E: