题目内容
在区间(-1,1)内不是增函数的是( )
| A、y=ex+x |
| B、y=sinx |
| C、y=x3-6x2+9x+2 |
| D、y=x2+x+1 |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:根据指数函数,幂函数,三角函数的性质,可以找出在区间(-1,1)上不是增函数的函数.
解答:
解:根据指数函数,三角函数的性质可知y=ex+x,y=sinx,y=x3-6x2+9x+2在区间(1,1)上都是增函数,而y=x2+x+1=(x+
)2+
-1,在(-∞,-
)递增,在(
,+∞)递减.
故选:D.
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
故选:D.
点评:本题主要考查了指数函数、幂函数及三角函数的单调性的判断,解题的关键是熟练掌握基本初等函数的单调性的结论.

练习册系列答案
相关题目
已知a=21.2,b=0.50.8,c=log23,则( )
| A、a>b>c |
| B、a>c>b |
| C、c>a>b |
| D、c>b>a |
在区间[-3,3]上任取一个数a,则圆C1:x2+y2+4x-5=0与圆C2:(x-a)2+y2=1有公共点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知P(-8,6)是角终边上一点,则2sinα+cosα的值等于( )
A、
| ||
B、-
| ||
C、-
| ||
D、
|
如图所示程序运行的结果是( )


| A、-2 | B、1 | C、4 | D、8 |
已知集合A={2,3},B={x|x2-5x+6≤0},则A∩B=( )
| A、{2,3} | B、[2,3] |
| C、{2} | D、{3} |
函数f(x)=(x2-1)cos2x在区间[0,2π]上的零点个数为( )
| A、6 | B、5 | C、4 | D、3 |

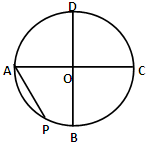 如图,圆O的半径为1,AC⊥BD,动点P从点A出发,沿圆弧
如图,圆O的半径为1,AC⊥BD,动点P从点A出发,沿圆弧