题目内容

设a=log23，b=2
3
2
，c=3-
4
3
，则（　　）
A、b＜a＜c
B、c＜a＜b
C、c＜b＜a
D、a＜c＜b
考点：对数值大小的比较
专题：函数的性质及应用
分析：利用对数函数和指数函数的单调性比较大小．
解答： 解：∵1＜a=log23＜2，b=2
3
2
＞2，c=3-
4
3
＜1，
∴c＜a＜b．
故选：B．
点评：本题考查三个数的大小的比较，是基础题，解题时要认真审题，注意对数函数和指数函数的单调性的合理运用．
练习册系列答案
相关题目
如果a⊥b，那么a与b（　　）
A、一定相交B、一定异面
C、一定共面D、一定不平行
已知O是△ABC所在平面内一点，且满足|
OB
-
OC
|=|
OB
+
OC
-2
OA
|，若|AB|=2，|AC|=
3
，则△ABC的外接圆的面积为
 
．
设x∈R，用[x]表示不超过x的最大整数，称函数f（x）=[x]为高斯函数，也叫取整函数．现有下列四个命题：
①高斯函数为定义域为R的奇函数；
②“[x]”≥“[y]”是“x≥y”的必要不充分条件；
③设g（x）=（
1
2
）|x|，则函数f（x）=[g（x）]的值域为{0，1}；
④方程[
x+1
4
]=[
x-1
2
]的解集是{x|1≤x＜5}．
其中真命题的序号是
 
．（写出所有真命题的序号）
把下列各数a=（
5
3
） 
1
3
，b=2 
2
3
，c=（-
2
3
） 
1
3
，d=（
3
5
） 
1
2
，按从小到大的顺序排列为
 
．
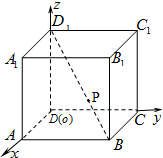如图在棱长为1正方体ABCD-A1B1C1D1中，以正方体的三条棱所在直线为轴建立空间直角坐标系Oxyz，
（I）若点P在线段BD1上，且满足3|BP|=|BD1|，试写出点P的坐标并写出P关于平面Oxz的对称点P′的坐标；
（Ⅱ）线段C1D中点为M，求点M到点P的距离．
设函数f（x）是定义在R上的周期为2的函数，且当x∈[-1，1）时，f（x）=
-2x2-x+2，-1≤x＜0
2x-1，0≤x＜1
，f（5）=
 
．
若函数f（
2x
+1）=x2-2x，则f（3）=（　　）
A、0B、1C、2D、3
已知函数f（x）=2x-（
1
2
）|x|，若f（x）=2，求2x的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网