题目内容
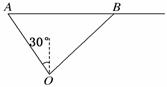 如图所示,在某港口O要将一件重要物 品用小艇送到一艘正在航行的轮船上, 在小艇出发时,轮船位于港口O北偏西 30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
如图所示,在某港口O要将一件重要物 品用小艇送到一艘正在航行的轮船上, 在小艇出发时,轮船位于港口O北偏西 30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值;
解:(1)设相遇时小艇航行距离为S海里,则
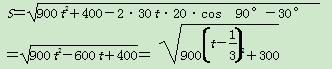 故当t=
故当t=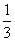 时,Smin=10
时,Smin=10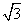 ,v=30
,v=30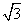 ,即小艇以每小时30
,即小艇以每小时30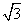
海里的速度航行,相遇时距离最小.
(2)若轮船与小艇在B处相遇,由题意可得:
(vt)2=202+(30t)2-2·20·(30t)·cos(90°-30°)
化简得v2=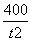 -
-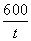 +900=400
+900=400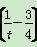 2+675,
2+675,
由于0<t≤ ,即
,即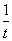 ≥2,所以当
≥2,所以当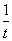 =2时,v取得最小值10
=2时,v取得最小值10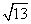 ,
,
即小艇航行速度的最小值为10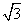 海里/小时.
海里/小时.

练习册系列答案
相关题目
 ”是真命题,则实数a的取值范围是
”是真命题,则实数a的取值范围是  为偶函数,
为偶函数, ,其图象与直线
,其图象与直线 的某两个交点的横坐标为
的某两个交点的横坐标为 ,若|
,若| |的最小值为
|的最小值为 ,则( )
,则( ) B.
B.  C.
C.  D.
D. 
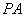 与⊙
与⊙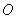 相切,
相切,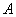 为切点,过点
为切点,过点 的割线交圆于
的割线交圆于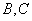 两点,弦
两点,弦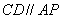 ,
, 相交于点
相交于点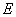 ,
,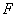 为
为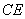 上一点,且
上一点,且 .
.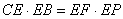 ;
;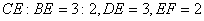 ,求
,求
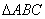 中,内角
中,内角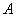 ,
,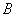 ,
,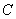 的对边分别为
的对边分别为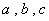 .已知
.已知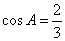 ,
,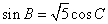
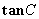 的值;(2)若
的值;(2)若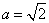 ,求
,求 矩阵,且规定其元素
矩阵,且规定其元素 ,其中
,其中 ,那么A中所有元素之和为 .
,那么A中所有元素之和为 . ,则
,则 = .
= . 与
与 的夹角为
的夹角为 ,
, 则
则 ( )
( ) B
B  C 4 D 12
C 4 D 12