题目内容
正四棱锥S-ABCD底面边长为2,高为1,E是边BC的中点,动点P在四棱锥表面上运动,并且总保持
•
=0,则动点P的轨迹的周长为 .
| PE |
| AC |
考点:轨迹方程
专题:计算题,空间位置关系与距离
分析:根据题意可知点P的轨迹为三角形EFG,其中G、F为中点,根据中位线定理求出EF、GE、GF,从而求出轨迹的周长.
解答:
解:由题意知:点P的轨迹为如图所示的三角形EFG,其中G、F为中点,
∴EF=
BD=
,
∵SB=
=
,
∴GE=GF=
SB=
,
∴轨迹的周长为
+
.
故答案为:
+
.

∴EF=
| 1 |
| 2 |
| 2 |
∵SB=
| 2+1 |
| 3 |
∴GE=GF=
| 1 |
| 2 |
| ||
| 2 |
∴轨迹的周长为
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题主要考查了轨迹问题,以及点到面的距离等有关知识,同时考查了空间想象能力,计算推理能力,属于中档题.

练习册系列答案
相关题目
如图所示,则阴影部分的面积为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
在如图所示的程序框图中,若f0(x)=xex,则输出的结果是( )
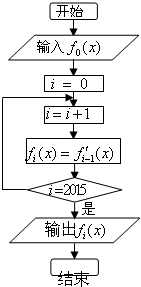

| A、2016ex+xex |
| B、2015ex+xex |
| C、2014ex+xex |
| D、2013ex+x |
在△ABC中,角A、B、C所对的边分别为a,b,c,且
=
,则角C是( )
| sinA |
| a |
| ||
| c |
A、
| ||
B、
| ||
C、
| ||
D、
|