题目内容

9．5051-1被7除后的余数为0．

分析 根据5051-1=（49+1）51-1，按照二项式定理展开，可得它除以7的余数．

解答 解：5051-1=（49+1）51-1=${C}_{51}^{0}$•4951+${C}_{51}^{1}$•4950+${C}_{51}^{2}$•4949+…+${C}_{51}^{50}$•49+${C}_{51}^{51}$-1，
显然，除了最后两项外，其余的各项都能被7整除，故它除以7的余数为 ${C}_{51}^{51}$-1=0，
故答案为：0．

点评 本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，属于基础题．

练习册系列答案
相关题目
19．设数列{an}的前n项的和为Sn，已知a1=$\frac{3}{2}$，an+1=$\frac{{a}_{n}^{3}}{2{a}_{n}^{2}-3{a}_{n}+2}$，其中n∈N*．
（1）证明：an＜2；
（2）证明：an＜an+1；
（3）证明：2n-$\frac{4}{3}$≤Sn≤2n-1+（$\frac{1}{2}$）n．
20．已知数列{an}满足${a_n}•{a_{n+1}}=\frac{n}{n+2}，（n∈{N^*}）$，${a_1}=\frac{1}{2}$．
（1）求a2，a3，a4值；
（2）归纳猜想数列{an}的通项公式，并用数学归纳法证明．
17．已知数列{an}中，an=-3n+4，等比数列{bn}的公比q满足q=an-an-1（n≥2）且b1=a1，则满足$\frac{1}{{|{b_1}|}}+\frac{1}{{|{b_2}|}}+…+\frac{1}{{|{b_n}|}}＜\frac{121}{81}$成立的n的最大值为（　　）
A．3B．4C．5D．6
4．已知中心在原点，对称轴为坐标轴的椭圆C的一个焦点F在抛物线y2=4x的准线上，且椭圆C过点$P（1，\frac{3}{2}）$，直线与椭圆C交于A，B两个不同点．
（1）求椭圆C的方程；
（2）若直线的斜率为$\frac{1}{2}$，且不过点P，设直线PA，PB的斜率分别为k1，k2，求证：k1+k2为定值．
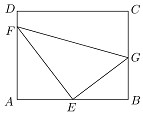14．如图，某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道（直角△EFG，E是直角顶点）来处理污水，管道越长，污水净化效果越好，设计要求管道的接口E是AB的中点，F、G分别落在AD、BC上，且AB=20m，$AD=10\sqrt{3}m$，设∠GEB=θ．
（1）试将污水管道的长度l表示成θ的函数，并写出定义域；
（2）当θ为何值时，污水净化效果最好，并求此时管道的长度．
1．若数列{an}是正项数列，且$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+$\sqrt{{a}_{3}}$+…+$\sqrt{{a}_{n}}$=n2+n，则$\frac{1}{{a}_{1}-1}$+$\frac{1}{{a}_{2}-1}$+…+$\frac{1}{{a}_{n}-1}$=$\frac{n}{2n+1}$．
18．已知R为实数集，集合A={x|x2-2x≥0}，B={x|x＞1}，则（∁RA）∩B（　　）
A．（0，1）B．（0，1]C．（1，2）D．（1，2]
15．已知向量$\overrightarrow{a}$=（sinx，-1），$\overrightarrow{b}$=$（{\sqrt{3}cosx，-\frac{1}{2}}）$．函数f（x）=（$\overrightarrow{a}$+$\overrightarrow{b}$）•$\overrightarrow{a}$-2．
（1）求函数f（x）的单调递减区间；
（2）已知a，b，c分别为△ABC内角A，B，C 的对边，其中A为锐角，a=2$\sqrt{3}$，c=4，且f（A）=1，求△ABC的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网