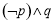题目内容
7.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )
| A. | $28+4\sqrt{3}+12\sqrt{2}$ | B. | $36+4\sqrt{3}+12\sqrt{2}$ | C. | $36+4\sqrt{2}+12\sqrt{3}$ | D. | $44+12\sqrt{2}$ |
分析 由三视图还原原几何体如图,该几何体下底面是等腰直角三角形,直角边为4,上底面是等腰直角三角形,直角边为2$\sqrt{2}$.CG⊥底面ABC,CG⊥底面EFG.然后结合三角形、正方形及梯形面积求解.
解答 解:由三视图还原原几何体如图: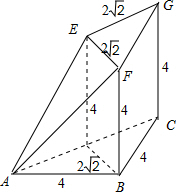
下底面是等腰直角三角形,直角边为4,上底面是等腰直角三角形,直角边为2$\sqrt{2}$.
CG⊥底面ABC,CG⊥底面EFG.
可求得AE=AF=4$\sqrt{2}$.
∴等腰三角形AEF底边上的高为$\sqrt{(4\sqrt{2})^{2}-(2\sqrt{2})^{2}}=2\sqrt{6}$.
∴该几何体的表面积为S=$\frac{1}{2}×4×4+\frac{1}{2}×2\sqrt{2}×2\sqrt{2}$$+\frac{1}{2}×4×4+4×4+\frac{1}{2}×2\sqrt{2}×2\sqrt{6}$$+\frac{1}{2}(2\sqrt{2}+4\sqrt{2})×4$=$36+4\sqrt{3}+12\sqrt{2}$.
故选:B.
点评 本题考查几何体的三视图,关键是由三视图还原原几何体,是中档题.

练习册系列答案
相关题目
17.设函数f(x)的定义域是R,则“?x∈R,f(x+2)>f(x)”是“函数f(x)为增函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
15.函数y=xsinx+cosx的导数为( )
| A. | -xcosx | B. | xcosx | C. | -xsinx | D. | xsinx |
12.已知双曲线C的中点在原点O,焦点$F({-2\sqrt{5},0})$,点A为左支上一点,满足|OA|=|OF|且|AF|=4,则双曲线C的方程为( )
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{36}-\frac{y^2}{16}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{16}=1$ | D. | $\frac{x^2}{16}-\frac{y^2}{36}=1$ |
 .
. ;
; ,求证:
,求证: ,
, 恒成立.
恒成立. ,则
,则 ( )
( )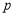 :对任意
:对任意 ,
,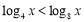 ,命题
,命题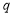 :存在
:存在 ,使得
,使得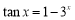 ,则下列命题为真命题的是( )
,则下列命题为真命题的是( )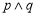 B.
B.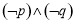
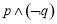 D.
D.