题目内容
17.已知偶函数f(x)在[0,+∞)单调递减,f(2)=0.若x•f(x-1)>0,则x的取值范围是(-∞,-1)∪(0,3).分析 根据函数奇偶性和单调性之间的关系将不等式等价转化为x>0时f(x-1)>f(2),x<0时,f(x-1)<f(-2),即可得到结论.
解答 解:∵偶函数f(x)在[0,+∞)单调递减,f(2)=0,
∴f(x)在(-∞,0)递增,f(-2)=0;
∴x>0时,不等式xf(x-1)>0等价为f(x-1)>f(2),
即x-1<2,解得:0<x<3;
x<0时:不等式xf(x-1)>0等价为f(x-1)<f(-2),
即x-1<-2,解得:x<-1,
故答案为:(-∞,-1)∪(0,3).
点评 本题主要考查函数奇偶性和单调性之间的关系的应用,将不等式等价转化为f(x-1)>f(2)或f(x-1)<f(-2)是解决本题的关键.

练习册系列答案
相关题目

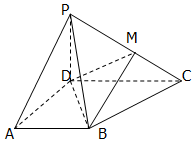 如图,四棱锥P-ABCD中,底面ABCD为梯形,∠DAB=60°,AB∥CD,AD=CD=2AB=2,PD⊥底面ABCD,M为PC的中点.
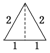
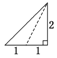
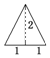
如图,四棱锥P-ABCD中,底面ABCD为梯形,∠DAB=60°,AB∥CD,AD=CD=2AB=2,PD⊥底面ABCD,M为PC的中点.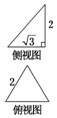 已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的正视图可能为( )
已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的正视图可能为( )