题目内容
12.已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=5,则2$\overrightarrow{a}$-$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
分析 根据平面向量数量积的定义与投影的定义,进行计算即可.
解答 解:∵向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,且|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=5,
∴(2$\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=2${\overrightarrow{a}}^{2}$-$\overrightarrow{b}$•$\overrightarrow{a}$=2×22-5×2×cos60°=3,
∴向量2$\overrightarrow{a}$-$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为$\frac{\overrightarrow{a}•(2\overrightarrow{a}-\overrightarrow{b})}{|\overrightarrow{a}|}$=$\frac{3}{2}$.
故选:A.
点评 本题考查了平面向量数量积的定义与投影的计算问题,是基础题目.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
3.定义在R上的函数f(x)满足:f(x+4)=f(x),f(x)=$\left\{\begin{array}{l}{2x,x∈(-1.1]}\\{-{x}^{2}+2x+1,x∈(1,3]}\\{\;}\end{array}\right.$,当x∈[0,+∞)时,方程f(x)-4xa=0(a>0)有且只有3个不等实根,则实数a的值为(e是自然对数底数)( )
| A. | $\frac{1}{{2}^{8}eln2}$ | B. | $\frac{1}{{2}^{9}}$ | C. | $\frac{e}{{2}^{8}ln2}$ | D. | $\frac{e}{{2}^{9}}$ |
20.正态分布ξ~N(a,32),且P(ξ<2a-3)=P(ξ>a+2),则a的值为( )
| A. | $\frac{7}{3}$ | B. | $\frac{4}{3}$ | C. | 1 | D. | 4 |
20.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F作一条直线,当直线倾斜角为$\frac{π}{6}$时,直线与双曲线左、右两支各有一个交点;当直线倾斜角为$\frac{π}{3}$时,直线与双曲线右支有两个不同的交点,则双曲线离心率的取值范围为( )
| A. | $({1,\frac{{2\sqrt{3}}}{3}})$ | B. | $({\frac{{2\sqrt{3}}}{3},2})$ | C. | $(1,\sqrt{3})$ | D. | (1,2) |
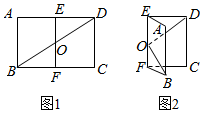 如图1,已知矩形ABCD中,AB=2,AD=2$\sqrt{2}$,E,F分别是AD,BC的中点,对角线BD与EF交于O点,沿EF将矩形ABFE折起,使平面ABFE与平面EFCD所成角为60°.在图2中:
如图1,已知矩形ABCD中,AB=2,AD=2$\sqrt{2}$,E,F分别是AD,BC的中点,对角线BD与EF交于O点,沿EF将矩形ABFE折起,使平面ABFE与平面EFCD所成角为60°.在图2中: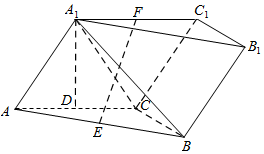 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,BC=1,且AC⊥BC,点D,E,F分别为AC,AB,A1C1的中点.
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,BC=1,且AC⊥BC,点D,E,F分别为AC,AB,A1C1的中点. 如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,AM=2.
如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,AM=2.