题目内容
11．某公司为适应市场需求，投入98万元引进新生产设备，并马上投入生产，第一年需要的各种费用是12万元，从第二年开始，所需费用比上一年增加4万元，而每年因引入该设备可获得的年利润为50万元，则引进该设备3年后，该公司开始盈利．分析 设引进该设备 n年后，该公司开始盈利，则50n＞98+12n+$\frac{n（n-1）}{2}×4$，解出即可得出．
解答 解：设引进该设备 n年后，该公司开始盈利，则50n＞98+12n+$\frac{n（n-1）}{2}×4$，
化为：n2-20n+49＜0，解得10-$\sqrt{15}$＜n＜$10+\sqrt{51}$，
∴引进该设备3年后，该公司开始盈利．
故答案为：3．
点评 本题考查了等差数列的通项公式与求和公式、不等式的解法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
1．已知i为虚数单位，m∈R，复数z=（-m2+2m+8）+（m2-8m）i，若z为负实数，则m的取值集合为（ ）
| A． | {0} | B． | {8} | C． | （-2，4） | D． | （-4，2） |
2．直线MN的斜率为2，其中点N（1，-1），点M在直线y=x+1上，则（ ）
| A． | M（5，7） | B． | M（4，5） | C． | M（2，1） | D． | M（2，3） |
19．设集合U={0，1，2，3，4，5}，A={1，2，3}，B={x∈Z|x2-5x+4≥0}，则A∩（∁UB）=（ ）
| A． | {1，2，3} | B． | {1，2} | C． | {2，3} | D． | {2} |
6．
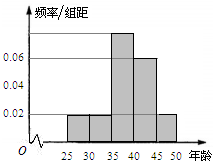某单位N名员工参加“我爱阅读”活动，他们的年龄在25岁至50岁之间，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50），得到的频率分布直方图如图所示．
（Ⅰ）求正整数a，b，N的值；
（Ⅱ）现要从年龄低于40岁的员工用分层抽样的方法抽取42人，则年龄在第1，2，3组得员工人数分别是多少？
（Ⅲ）为了估计该单位员工的阅读倾向，现对该单位所有员工中按性别比例抽查的40人是否喜欢阅读国学类书
籍进行了调查，调查结果如下所示：（单位：人）
下面是年龄的分布表：
根据表中数据，我们能否有99%的把握认为该位员工是否喜欢阅读国学类书籍和性别有关系？
附：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$，其中n=a+b+c+d．
某单位N名员工参加“我爱阅读”活动，他们的年龄在25岁至50岁之间，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50），得到的频率分布直方图如图所示．（Ⅰ）求正整数a，b，N的值；
（Ⅱ）现要从年龄低于40岁的员工用分层抽样的方法抽取42人，则年龄在第1，2，3组得员工人数分别是多少？
（Ⅲ）为了估计该单位员工的阅读倾向，现对该单位所有员工中按性别比例抽查的40人是否喜欢阅读国学类书
| 喜欢阅读国学类 | 不喜欢阅读国学类 | 合计 | |
| 男 | 14 | 4 | 18 |
| 女 | 8 | 14 | 22 |
| 合计 | 22 | 18 | 40 |
下面是年龄的分布表：
| 区间 | [25，30） | [30，35） | [35，40） | [40，45） | [45，50） |
| 人数 | 28 | a | b |
附：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$，其中n=a+b+c+d．
| P（K2≥k0） | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
16．已知f（x）是定义在R上的可导函数，且满足（x+2）f（x）+xf'（x）＞0，则（ ）
| A． | f（x）＞0 | B． | f（x）＜0 | C． | f（x）为减函数 | D． | f（x）为增函数 |
20．已知双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$，若正方形ABCD四个顶点在双曲线C上，且AB，CD的中点为双曲线C的两个焦点，则双曲线C的离心率为（ ）
| A． | $\frac{{\sqrt{5}-1}}{2}$ | B． | $\sqrt{5}-1$ | C． | $\frac{{\sqrt{5}+1}}{2}$ | D． | $\sqrt{5}+1$ |
1．已知cos（$\frac{2π}{3}$-α）=$\frac{3}{4}$，则sin（α-$\frac{π}{6}$）cos（$\frac{π}{3}$-2α）=（ ）
| A． | $\frac{3}{32}$ | B． | -$\frac{3}{32}$ | C． | $\frac{3}{16}$ | D． | -$\frac{3}{16}$ |