题目内容

设双曲线
y2
9
-
x2
a2
=1（a＞0）的渐近线方程为3x±2y=0，则a的值为（　　）
A、4B、3C、2D、9/2
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由双曲线的方程求出其实半轴和虚半轴的长，结合其渐近线方程得答案．
解答： 解：由双曲线
y2
9
-
x2
a2
=1（a＞0），的双曲线的实半轴长为3，虚半轴长为a，
∵双曲线
y2
9
-
x2
a2
=1（a＞0）的渐近线方程为3x±2y=0，
即y=±
3
2
x，
∴
3
a
=
3
2
，a=2．
故选：C．
点评：本题考查了双曲线的简单几何性质，考查了双曲线的渐近线方程，是基础题．
练习册系列答案
相关题目
已知函数y=
x-2
x-1
，则（　　）
A、（-∞，1）是函数的递增区间
B、（-∞，-1）是函数的递减区间
C、（-1，+∞）是函数的递增区间
D、（1，+∞）是函数的递减区间
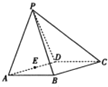如图，四棱锥P-BCDE中，四边形ABCD为菱形，且∠DAB=60°，△PAD为对边三角形，平面PAD⊥平面ABCD，AB=2，E为AD的中点．
（1）求证：AD⊥PB；
（2）求点E到平面PBC的距离．
已知数列{an}的前n项和为Sn，若Sn+n=
3
2
an．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设数列{bn}满足bn=an+λ（-2）n且数列{bn}为递增数列，求λ的取值范围．
某环保部门对某处的环境情况用“污染指数”来监测，据测定，该处的“污染指数”与附近污染源的强度和距离之比成正比，比例常数为k（k＞0）．现已知相距36km的A，B两家化工厂（污染源）的污染强度分别为正数1，a，它们连线上任意一点C处的污染指数y等于两化工厂对该处的污染指数之和．设AC=x（km）．
（1）试将y表示为x的函数，指出其定义域；
（2）当x=6时，C处“污染指数”最小，试求B化工厂的污染强度a的值．
已知过点A（-2，-4）且斜率为1的直线l交抛物线y2=2px（p＞0）于B，C两点，若AB、BC、CA的绝对值成等比数列，求抛物线方程．
设
a
、
b
、
c
有公共起点
c
=m
a
+n
b
，要使
a
、
b
、
c
的终点在一条直线上，则m n应满足
 
条件．
在装有相同数量的白球和黑球的口袋中放进1个白球，此时由这个口袋中取出1个白球的概率比口袋中原来取出一个白球的概率大0.1，则口袋中原有球的个数是（　　）
A、2B、4C、8D、10
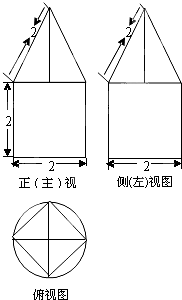一空间几何体的三视图如图所示，则该几何体的表面积为（　　）
A、6π+4
2
-2
B、6π+4
2
C、2π+
2
3
3
D、2π+4
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网