题目内容
已知函数y=
,则( )
| x-2 |
| x-1 |
| A、(-∞,1)是函数的递增区间 |
| B、(-∞,-1)是函数的递减区间 |
| C、(-1,+∞)是函数的递增区间 |
| D、(1,+∞)是函数的递减区间 |
考点:函数单调性的判断与证明
专题:导数的综合应用
分析:求y′,并可判断y′>0,而该函数的定义域为(-∞,1)∪(1,+∞),所以得到(-∞,1)是该函数的递增区间.
解答:
解:y′=
>0;
∴该函数在(-∞,1),(1,+∞)上单调递增;
即(-∞,1),(1,+∞)是该函数的单调递增区间.
故选A.
| 1 |
| (x-1)2 |
∴该函数在(-∞,1),(1,+∞)上单调递增;
即(-∞,1),(1,+∞)是该函数的单调递增区间.
故选A.
点评:考查根据函数导数符号判断函数单调性及判断出函数单调区间的方法,注意单调区间是连续的.

练习册系列答案
相关题目
下列函数中,既是偶函数又在(0,+∞)上是增函数的是( )
| A、y=|x|+1 | ||
B、y=-
| ||
| C、y=-x2+1 | ||
| D、y=2-x |
设集合A={-1,0,1},B={1,4},则A∪B=( )
| A、{1} |
| B、{-1,0,4} |
| C、{-1,0,1,4} |
| D、{0,1,4} |
给出以下命题,不正确的是( )
| A、如果两条平行线中的一条与一个平面相交,那么另一条也和这个平面相交 |
| B、如果直线a和直线b平行,那么直线a平行于经过b的所有的平面 |
| C、如果a和b是异面直线,那么经过a有且只有一个平面与直线b平行 |
| D、空间四边形相邻两边的中点连线,平行于经过另外两条边的平面 |
设双曲线
-
=1(a>0)的渐近线方程为3x±2y=0,则a的值为( )
| y2 |
| 9 |
| x2 |
| a2 |
| A、4 | B、3 | C、2 | D、9/2 |
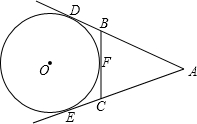 如图:AE、AD、BC分别切⊙O于E、D、F,若AD=18,则△ABC的周长为
如图:AE、AD、BC分别切⊙O于E、D、F,若AD=18,则△ABC的周长为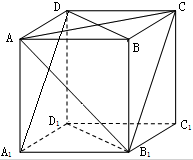 如图,ABCD-A1B1C1D1是棱长为1的正方体.
如图,ABCD-A1B1C1D1是棱长为1的正方体.