题目内容
已知函数f（x）=
，若f（a）+f（f（1））=0，则实数a的值等于（ ）
|
| A、-28 | B、-10 |
| C、10 | D、28 |
考点：函数的值
专题：函数的性质及应用
分析：由已知得f（1）=2，f（f（1））=f（2）=32=9，从而f（a）=-9．由此利用分段函数的性质能求出a．
解答：
解：∵函数f（x）=
，
∴f（1）=2，f（f（1））=f（2）=32=9，
∵f（a）+f（f（1））=0，
∴f（a）=-9．
当a＞1时，3a=-9，不成立；
当a≤1时，a+1=-9，解得a=-10．
故选：B．
|
∴f（1）=2，f（f（1））=f（2）=32=9，
∵f（a）+f（f（1））=0，
∴f（a）=-9．
当a＞1时，3a=-9，不成立；
当a≤1时，a+1=-9，解得a=-10．
故选：B．
点评：本题考查实数值的求法，是基础题，解题时要认真审题．
练习册系列答案
相关题目
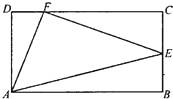如图所示，有一个长AB=4，宽BC=2的矩形木料ABCD，E为BC的中点，点F在边CD上．一木工师傅想在该木料上取满足∠EAF=| π |
| 3 |
A、（
| ||||
B、（
| ||||
C、（
| ||||
D、（0，
|
（文科）已知A（x1，y1）、B（x2，y2）为抛物线y2=4x上两个不同的点，且y1y2=-8，则x1x2的值为（ ）
| A、8 | B、4 | C、-8 | D、-4 |
定义在R上的奇函数f（x）满足f（x+3）=f（x），当0＜x≤1时，f（x）=2x，则f（2）=（ ）
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
已知条件p：|x-1|＜2，条件q：x2-3x-4＜0，则条件p成立是条件q成立的（ ）
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
已知命题p：?x∈（1，+∞），函数f（x）=log2（x+1）-1有零点；命题q：若a=（1，2），b=（-2，-4），则a∥b，下列命题为真命题的是（ ）
| A、p∧q |
| B、p∨（￢q） |
| C、（￢p）∧q |
| D、p∧（￢q） |